Информатика Логика Законы
Оглавление:
Законы логики на уроках информатики и ИКТ
Урок по информатике рассчитан на учащихся 10-х классов общеобразовательной школы, в учебном плане которой входит раздел «Алгебра логики». Учащимся очень нелегко дается эта тема, поэтому мне, как учителю, захотелось заинтересовать их в изучении законов логики, упрощении логических выражений и с интересом подойти к решению логических задач. В обычной форме давать уроки по этой теме нудно и хлопотно, да и ребятам не всегда понятны некоторые определения. В связи с предоставлением информационного пространства, у меня появилась возможность выкладывать свои уроки в оболочке «learning». Учащиеся, зарегистрировавшись в ней, могут в свое свободное время посещать этот курс и перечитывать то, что было непонятно на уроке. Некоторые учащиеся, пропустив уроки по болезни, наверстывают дома или в школе пропущенную тему и всегда готовы к следующему уроку. Такая форма преподавания очень устроила многих ребят и те законы, которые им были непонятны, теперь в компьютерном виде ими усваиваются гораздо легче и быстрее. Предлагаю один из таких уроков информатики, который проводится интегративно с ИКТ.
1. Объяснение нового материала
Законы формальной логики
Наиболее простые и необходимые истинные связи между мыслями выражаются в основных законах формальной логики. Таковыми являются законы тождества, непротиворечия, исключенного третьего, достаточного основания.
Эти законы являются основными потому, что в логике они играют особо важную роль, являются наиболее общими. Они позволяют упрощать логические выражения и строить умозаключения и доказательства. Первые три из вышеперечисленных законов были выявлены и сформулированы Аристотелем, а закон достаточного основания — Г. Лейбницем.
Закон тождества: в процессе определенного рассуждения всякое понятие и суждение должны быть тождественны самим себе.
Закон непротиворечия: невозможно, чтобы одно и то оке в одно то же время было и не было присуще одному и тому же в одном и том же отношении. То есть невозможно что-либо одновременно утверждать и отрицать.
Закон исключенного третьего: из двух противоречащих суждений одно истинно, другое ложно, а третьего не дано.
Закон достаточного основания: всякая истинная мысль должна быть достаточно обоснована.
Последний закон говорит о том, что доказательство чего-либо предполагает обоснование именно и только истинных мыслей. Ложные же мысли доказать нельзя. Есть хорошая латинская пословица: «Ошибаться свойственно всякому человеку, но настаивать на ошибке свойственно только глупцу». Формулы этого закона нет, так как он имеет только содержательный характер. В качестве аргументов для подтверждения истинной мысли могут быть использованы истинные суждения, фактический материал, статистические данные, законы науки, аксиомы, доказанные теоремы.
Законы алгебры высказываний
Алгебра высказываний (алгебра логики) — раздел математической логики, изучающий логические операции над высказываниями и правила преобразования сложных высказываний.
При решении многих логических задач часто приходится упрощать формулы, полученные при формализации их условий. Упрощение формул в алгебре высказываний производится на основе эквивалентных преобразований, опирающихся на основные логические законы.
Законы алгебры высказываний (алгебры логики) — это тавтологии.
Иногда эти законы называются теоремами.
В алгебре высказываний логические законы выражаются в виде равенства эквивалентных формул. Среди законов особо выделяются такие, которые содержат одну переменную.
Первые четыре из приведенных ниже законов являются основными законами алгебры высказываний.
Всякое понятие и суждение тождественно самому себе.
Закон тождества означает, что в процессе рассуждения нельзя подменять одну мысль другой, одно понятие другим. При нарушении этого закона возможны логические ошибки.
Например, рассуждение Правильно говорят, что язык до Киева доведет, а я купил вчера копченый язык, значит, теперь смело могу идти в Киев неверно, так как первое и второе слова «язык» обозначают разные понятия.
В рассуждении: Движение вечно. Хождение в школу — движение. Следовательно, хождение в школу вечно слово «движение» используется в двух разных смыслах (первое — в философском смысле — как атрибут материи, второе — в обыденном смысле — как действие по перемещению в пространстве), что приводит к ложному выводу.
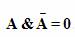
Не могут быть одновременно истинными суждение и его отрицание. То есть если высказывание А — истинно, то его отрицание не А должно быть ложным (и наоборот). Тогда их произведение будет всегда ложным.
Именно это равенство часто используется при упрощении сложных логических выражений.
Иногда этот закон формулируется так: два противоречащих друг другу высказывания не могут быть одновременно истинными. Примеры невыполнения закона непротиворечия:
1. На Марсе есть жизнь и на Марсе жизни нет.
2. Оля окончила среднюю школу и учится в X классе.
Закон исключенного третьего:
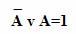
В один и тот же момент времени высказывание может быть либо истинным, либо ложным, третьего не дано. Истинно либо А, либо не А. Примеры выполнения закона исключенного третьего:
1. Число 12345 либо четное, либо нечетное, третьего не дано.
2. Предприятие работает убыточно или безубыточно.
3. Эта жидкость является или не является кислотой.
Закон исключенного третьего не является законом, признаваемым всеми логиками в качестве универсального закона логики. Этот закон применяется там, где познание имеет дело с жесткой ситуацией: «либо — либо», «истина—ложь». Там же, где встречается неопределенность (например, в рассуждениях о будущем), закон исключенного третьего часто не может быть применен.
Рассмотрим следующее высказывание: Это предложение ложно. Оно не может быть истинным, потому что в нем утверждается, что оно ложно. Но оно не может быть и ложным, потому что тогда оно было бы истинным. Это высказывание не истинно и не ложно, а потому нарушается закон исключенного третьего.
Парадокс (греч. paradoxos — неожиданный, странный) в этом примере возникает из-за того, что предложение ссылается само на себя. Другим известным парадоксом является задача о парикмахере: В одном городе парикмахер стрижет волосы всем жителям, кроме тех, кто стрижет себя сам. Кто стрижет волосы парикмахеру? В логике из-за ее формальности нет возможности получить форму такого ссылающегося самого на себя высказывания. Это еще раз подтверждает мысль о том, что с помощью алгебры логики нельзя выразить все возможные мысли и доводы. Покажем, как на основании определения эквивалентности высказываний могут быть получены остальные законы алгебры высказываний.
Например, определим, чему эквивалентно (равносильно) А (двойное отрицание А, т. е. отрицание отрицания А). Для этого построим таблицу истинности:
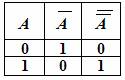
По определению равносильности мы должны найти тот столбец, значения которого совпадают со значениями столбца А. Таким будет столбец А.
Таким образом, мы можем сформулировать закон двойного отрицания:
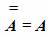
Если отрицать дважды некоторое высказывание, то в результате получается исходное высказывание. Например, высказывание А = Матроскин — кот эквивалентно высказыванию А = Неверно, что Матроскин не кот.
Аналогичным образом можно вывести и проверить следующие законы:
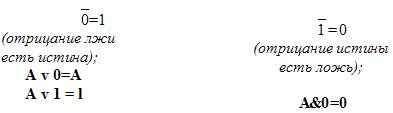
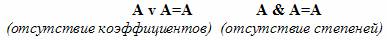
Сколько бы раз мы ни повторяли: телевизор включен или телевизор включен или телевизор включен . значение высказывания не изменится. Аналогично от повторения на улице тепло, на улице тепло. ни на один градус теплее не станет.
Операнды А и В в операциях дизъюнкции и конъюнкции можно менять местами.
A v(B v C) = (A v B) v C;
А & (В & C) = (A & В) & С.
Если в выражении используется только операция дизъюнкции или только операция конъюнкции, то можно пренебрегать скобками или произвольно их расставлять.
A v (B & C) = (A v B) &(A v C)
(дистрибутивность дизъюнкции
относительно конъюнкции)
А & (B v C) = (A & B) v (А & C)
(дистрибутивность конъюнкции
относительно дизъюнкции)
Закон дистрибутивности конъюнкции относительно дизъюнкции аналогичен дистрибутивному закону в алгебре, а закон дистрибутивности дизъюнкции относительно конъюнкции аналога не имеет, он справедлив только в логике. Поэтому необходимо его доказать. Доказательство удобнее всего провести с помощью таблицы истинности:
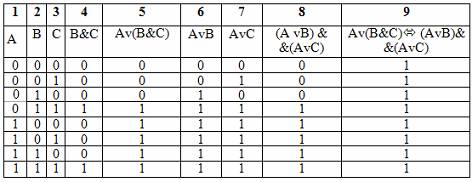
Проведите доказательство законов поглощения самостоятельно.
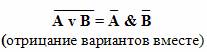
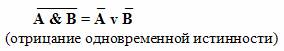
Словесные формулировки законов де Моргана:


Мнемоническое правило: в левой части тождества операция отрицания стоит над всем высказыванием. В правой части она как бы разрывается и отрицание стоит над каждым из простых высказываний, но одновременно меняется операция: дизъюнкция на конъюнкцию и наоборот.
Примеры выполнения закона де Моргана:
1) Высказывание Неверно, что я знаю арабский или китайский язык тождественно высказыванию Я не знаю арабского языка и не знаю китайского языка.
2) Высказывание Неверно, что я выучил урок и получил по нему двойку тождественно высказыванию Или я не выучил урок, или я не получил по нему двойку.
Замена операций импликации и эквивалентности
Операций импликации и эквивалентности иногда нет среди логических операций конкретного компьютера или транслятора с языка программирования. Однако для решения многих задач эти операции необходимы. Существуют правила замены данных операций на последовательности операций отрицания, дизъюнкции и конъюнкции.
Так, заменить операцию импликации можно в соответствии со следующим правилом:
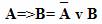
Для замены операции эквивалентности существует два правила:
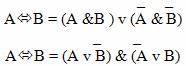
В справедливости данных формул легко убедиться, построив таблицы истинности для правой и левой частей обоих тождеств.
Знание правил замены операций импликации и эквивалентности помогает, например, правильно построить отрицание импликации.
Рассмотрим следующий пример.
Пусть дано высказывание:
Е = Неверно, что если я выиграю конкурс, то получу приз.
Пусть А = Я выиграю конкурс,
В = Я получу приз.
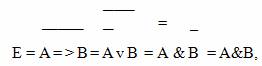
Отсюда, Е = Я выиграю конкурс, но приз не получу.
Интерес представляют и следующие правила:
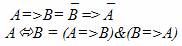
Доказать их справедливость можно также с помощью таблиц истинности.
Интересно их выражение на естественном языке.
Если Винни-Пух съел мед, то он сыт
Если Винни-Пух не сыт, то меда он не ел.
Задание: придумайте фразы-примеры на данные правила.
2. Основные понятия и определения в Приложении 1
3. Материал для любознательных в Приложении 2
4. Домашнее задание
1) Выучить законы логики, используя курс «Алгебры логики», размещенный в информационном пространстве (www.learning.9151394.ru).
2) Проверить на ПК доказательство законов де Моргана, построив таблицу истинности.
- Основные понятия и определения (Приложение 1).
- Материал для любознательных (Приложение 2).
- Обучающие:
- Изучить основные законы логики
- Научить преобразовывать логические выражения, используя логические законы
- Ввести понятие “нормальная форма логической формулы”
- Закрепить навыки упрощения логических выражений, используя логические законы
- Научить решать логические задачи
- Закрепить навыки решения логических задач
- Развивающие:
- Развивать логическое мышление
- Развивать внимание
- Развивать память
- Развивать речь учащихся
- Воспитывающие:
- Воспитывать умение слушать учителя и одноклассников
- Воспитывать аккуратность ведения тетради
- Воспитывать дисциплинированность
Ход урока
Здравствуйте, ребята. Мы продолжаем изучать основы логики и тема нашего сегодняшнего урока «Законы логики и правила преобразования логических выражений». Изучив данную тему, вы узнаете, основные законы логики, научитесь упрощать логические выражения, используя логические законы, решать логические задачи
Проверка домашнего задания
Какой у вас получился ответ в домашней задаче? (2)
Откройте свои тетради там, где вы выполняли домашнюю работу, я пройду посмотрю
Объяснение нового материала
Переходим к новой теме.
В алгебре логики имеется ряд законов, позволяющих производить равносильные преобразования логических выражений. Приведем соотношения, отражающие эти законы.
1. Закон двойного отрицания:
А =
 .
.Двойное отрицание исключает отрицание.
2. Переместительный (коммутативный) закон:
Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания.
В обычной алгебре 2 + 3 = 3 + 2, 2 ´ 3 = 3 ´ 2.
3. Сочетательный (ассоциативный) закон:
(A Ú B) Ú C = A Ú (BÚ C);
При одинаковых знаках скобки можно ставить произвольно или вообще опускать.
В обычной алгебре: (2 + 3) + 4 = 2 + (3 + 4) = 2 + 3 + 4, 5 ´ (6 ´ 7) = 5 ´ (6 ´ 7) = 5 ´ 6 ´ 7.
4. Распределительный (дистрибутивный) закон:
(A&B) Ú C = (A Ú C)&(B Ú C).
Определяет правило выноса общего высказывания за скобку.
В обычной алгебре: (2 + 3) ´ 4 = 2 ´ 4 + 3 ´4.
5. Закон общей инверсии (законы де Моргана):
— для логического сложения
 =
=  &
&  ;
; =
=  Ú
Ú 
6. Закон идемпотентности
Закон означает отсутствие показателей степени.
7. Законы исключения констант:
A Ú 1 = 1, A Ú 0 = A;
8. Закон противоречия:
A&
 = 0.
= 0.Невозможно, чтобы противоречащие высказывания были одновременно истинными.
9. Закон исключения третьего:
A Ú
 = 1.
= 1.10. Закон поглощения:
11. Закон исключения (склеивания):
— для логического сложения:
— для логического умножения:
(A Ú B)&(
 Ú B) = B.
Ú B) = B.12. Закон контрапозиции (правило перевертывания):
(A Û B) = (BÛ A).
┐(А→В) = А&┐В
┐А&(АÚВ)= ┐А&В
АÚ┐А&В=АÚВФормула имеет нормальную форму, если в ней отсутствуют знаки эквивалентности, импликации, двойного отрицания, при этом знаки отрицания находятся только при переменных.
Пример 1. Найдите X, если
 Ú
Ú  = В.
= В.Упростим левую часть равенства. Какими законами воспользуемся? Для преобразования левой части равенства последовательно воспользуемся законом де Моргана для логического сложения и законом двойного отрицания:
(
 &
&  ) Ú (
) Ú (  &A)
&A)Согласно распределительному закону для логического сложения:
 &(
&(  Ú A)
Ú A)Согласно закону исключения третьего и закона исключения констант:
 &1 =
&1 = 
Полученную левую часть приравняем правой:
 = В
= ВОкончательно получим, что
X =
 .
.Пример 2. Упростите логическое выражение (A Ú B Ú C)&

Посмотрите на выражение, посмотрите на законы, что можно сделать?
Согласно закону общей инверсии для логического сложения (первому закону Моргана) и закону двойного отрицания:
(A Ú B Ú C)&
 = (A Ú B Ú C)&(
= (A Ú B Ú C)&(  &B&
&B&  )
)Согласно распределительному (дистрибутивному) закону для логического сложения:
(A Ú B Ú C)&(
 &B&
&B&  ) = (A&
) = (A&  ) Ú (B&
) Ú (B&  ) Ú (C&
) Ú (C&  ) Ú (A&B) Ú (B&B) Ú (C&B) Ú (A&
) Ú (A&B) Ú (B&B) Ú (C&B) Ú (A&  ) Ú (B&
) Ú (B&  ) Ú (C&
) Ú (C&  )
)Согласно закона противоречия:
(A&
 ) = 0; (C&
) = 0; (C&  ) = 0
) = 0Согласно закона идемпотентности
Подставляем значения и, используя переместительный (коммутативный) закон и группируя слагаемые, получаем:
0 Ú (A&B) Ú (
 &B) Ú B Ú (C&B) Ú (
&B) Ú B Ú (C&B) Ú (  &B) Ú (C&
&B) Ú (C&  ) Ú (A&
) Ú (A&  ) Ú 0
) Ú 0Согласно закона исключения (склеивания)
(A&B) Ú (
 &B) = B
&B) = B
(C&B) Ú ( &B) = B
&B) = B0 Ú B Ú B Ú B Ú (C&
 ) Ú (A&
) Ú (A&  ) Ú 0
) Ú 0Согласно закона исключения констант для логического сложения и закона идемпотентности:
0 Ú B Ú 0 Ú B Ú B = B
Подставляем значения и получаем:
B Ú (C&
 ) Ú (A&
) Ú (A&  )
)Упростить логическую формулу:
Сегодня мы продолжаем изучать тему “Законы логики и правила преобразования логических выражений”. Будем упрощать выражения и учиться решать логические задачи
Но для начала проверим как вы выполнили домашнее задание (1 ученик у доски, остальные показывают в тетрадях).
1.Упростить логическое выражение
Чтобы проверить правильность упрощения, нужно построить таблицы истинности для исходного и полученного логического выражения. Результирующие столбцы должны совпадать.
2. Логическое выражение называется тождественно – ложным, если оно принимает значения 0 на всех наборах входящих в него простых высказываний.
Упростить выражение и показать, что оно тождественно – ложное
2.Логическое выражение называется тождественно – истинным, если оно принимает значения 1 на всех наборах входящих в него простых высказываний.
Упростить выражение и показать, что оно тождественно – истинное
3.Переведите к виду логической формулы высказывание: «Неверно, что если погода пасмурная, то дождь идет тогда и только тогда, когда нет ветра».
П — «пасмурная погода»;
Д — «идет дождь»;
В — «дует ветер».Тогда соответствующее логическое выражение запишется так:
Перейдем к решению логических задач. Логические задачи обычно формулируются на естественном языке. В первую очередь их необходимо формализовать, то есть записать на языке алгебры высказываний. Полученные логические выражения необходимо упростить и проанализировать. Для этого иногда бывает необходимо построить таблицу истинности полученного логического выражения. Несложные задачи решаются путем логических рассуждений.
В школе-новостройке в каждой из двух аудиторий может находиться либо кабинет информатики, либо кабинет физики. На дверях аудиторий повесили шутливые таблички. На первой повесили табличку «По крайней мере, в одной из этих аудиторий размешается кабинет информатики», а на второй аудитории — табличку с надписью «Кабинет физики находится в другой аудитории». Проверяющему, который пришел в школу, известно только, что надписи на табличках либо обе истинны, либо обе ложны. Помогите проверяющему найти кабинет информатики.
Переведем условие задачи на язык логики высказывании. Так как в каждой из аудиторий может находиться кабинет информатики, то пусть:
А = «В первой аудитории находится кабинет информатики»;
В = «Во второй аудитории находится кабинет информатики».Отрицаний этих высказывании:
А = «В первой аудитории находится кабинет физики»;
В = «Bo второй аудитории находится кабинет физики».Высказывание, содержащееся на табличке на двери первой аудитории, соответствует логическому выражению:
Высказывание, содержащееся на табличке на двери второй аудитории, соответствует логическому выражению:
Содержащееся в условии задачи утверждение о том, что надписи на табличках либо одновременно истинные, либо одновременно ложные в соответствии с законом исключенного третьего записывается следующим образом:
Подставим вместо X и Y соответствующие формулы:
(X &Y) v (X & Y) = ((А vB) &A)v ((A v B) & А).
Упростим сначала первое слагаемое. В соответствии с законом дистрибутивности умножения относительно сложения:
((А vB) &A) = A&A v B&A
В соответствии с законом непротиворечия:
A&A v B&A = 0 v В&А
Упростим теперь второе слагаемое. В соответствии с первым законом де Моргана и законом двойного отрицания:
(A v B) & А = А&В&А = А&А&В
В результате получаем:
(0 v В & A) v 0 = В& А.
Для того чтобы выполнялось равенство В & А = 1, В и А должны быть равны 1, то есть соответствующие им высказывания истинны.
Ответ: В первой аудитории находится кабинет физики, а во второй — кабинет информатики.
5. Упростить логические выражения. Правильность упрощения логических выражений проверить с помощью таблиц истинности для исходных и полученных логических формул.
В процессе составления расписания уроков учителя высказали свои пожелания. Учитель математики, высказал пожелание проводить первый или второй урок, учитель информатики — первый или третий, а учитель физики второй или третий урок. Сколько существует возможных вариантов расписания и каковы они?
Проверим, как вы выполнили домашнюю работу.
Продолжаем решать задачи и упрощать логические выражения
Кто из учеников А, В, С и D играет, а кто не играет в шахматы, если известно следующее:
- а) если А или В играет, то С не играет;
- б) если В не играет, то играют С и D;
- в) С играет
- А — «ученик А играет в шахматы»;
- В — «ученик В играет в шахматы»;
- С — «ученик С играет в шахматы»;
- D — «ученик D играет в шахматы».
- пересечение (часть элементов объема каждого понятия входит в объем другого понятия); например, «мальчик»–«болельщик»;
- тождество (полное совпадение объемов понятий);
- подчинение (объем одного понятия полностью входит в объем другого); например, «акула»–«рыба».
- соподчинение; например, «рыба»–«птица» (соподчинены понятию «животное»);
- противоположность (объект, не попадающий под одно понятие, может не попадать и под другое); например, «черный»–«белый»;
- противоречие (объект принадлежит объему либо одного, либо другого понятия); например, «светящийся объект»–«несветящийся объект».
Решение. Определим следующие простые высказывания:
Запишем произведение указанных сложных высказываний:
((A v В) → С) & (В → С & D) & С.
Упростим эту формулу:
((A v В) → С) & (В → С & D) & С = ((А v В) v С) & (В v С & D) & С = (А & В) v С) & (В v С & D) & C = A & B & C & D =1.
Отсюда А = 0, В = 1, С = 1, D = 1.
Ответ: в шахматы играют ученики В,С и D, а ученик А не играет.
www.metodichka.net
В формальной логике предполагается, что в любом рассуждении можно разделить его содержание и форму. И, поскольку для определения правильности рассуждения важна только его форма, от содержания можно отвлечься.
Мыслить логично — значит мыслить точно и последовательно, не допускать противоречий в своих рассуждениях, уметь находить свои и чужие логические ошибки. Логичность мышления не гарантирует человеку, что он всегда будет знать истину, но позволит, по крайней мере, избежать очевидных ошибок.
Примерно также, вы, например, решая на уроке алгебры квадратное уравнение, не учитываете, что именно обозначают, входящие в него числа. И здесь тоже знание алгоритма решения не гарантирует правильность ответа в задаче (ведь ошибка могла быть допущена, к примеру, и при составлении уравнения), но резко повышает вероятность его получения.
Основные понятия логики
Понятие — форма мышления, в которой отражаются существенные отличительные признаки предметов.
Понятие имеет две основные логические характеристики: содержание и объем.Содержание понятия Содержанием понятия называется совокупность существенных признаков, отраженных в этом понятии. Объем понятия Объем понятия — это множество предметов, каждому из которых принадлежат признаки, относящиеся к содержанию понятия. Совместимые и несовместимые понятия По объему понятия могут быть совместимыми или несовместимыми. Объемы совместимых понятий совпадают полностью или частично (т.е. существуют объекты, имеющие признаки обоих понятий). Объемы несовместимых понятий не включают ни одного общего элемента.
Отношения совместимых понятий:
Отношения несовместимых понятий:
Высказывание
Высказывание (суждение) — форма мышления, в которой что-либо утверждается или отрицается о предметах, их свойствах, или отношениях.
Высказывание характеризуется своим содержанием и формой.Умозаключение
Умозаключение — форма мышления, посредством которой из одного или нескольких высказываний, называемых посылками, мы по определенным правилам вывода получаем заключение.
С точки зрения содержания мышление может давать истинное или ложное отражение мира, формально же оно может быть логически правильным или неправильным.
Логические операции
Высказывание, включающее другие высказывания, называют сложным. Для образования сложных высказываний используют логические операции (связки). Рассмотрим некоторые из них (в порядке приоритета при вычислении логических выражений).
Инверсия (отрицание) Инверсия — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда исходное высказывание ложно.
В выражениях обозначается ¬A или A .
Читается «НЕ» (например, «не А»). Конъюнкция (логическое умножение) Конъюнкция — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда истинны оба исходных высказывания.
В выражениях обозначается A ∧ B или A & B (знак может не указываться — AB).
Читается «И» (например, «А и Б») Дизъюнкция (логическое сложение) Дизъюнкция — это логическая операция, образующая сложное высказывание, истинное тогда, когда истинно хотя бы одно из исходных высказываний.
В выражениях обозначается A ∨ B, иногда A + B.
Читается «ИЛИ» (например, «А или Б») Импликация (следование) Импликация — это логическая операция, образующая сложное высказывание, ложное тогда и только тогда, когда первое исходное высказывание истинно, а второе — ложно.
В выражениях обозначается A ⇒ B или A → B.
Читается «ЕСЛИ. ТО» (например, «если А, то Б») Эквивалентность (равнозначность) Эквивалентность — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда значения исходных высказываний совпадают.
В выражениях обозначается A ⇔ B или A ≡ B.
Читается «ТОГДА И ТОЛЬКО ТОГДА, КОГДА» (например, «А тогда и только тогда, когда Б»)Для записи логических функций часто используют таблицы истинности.
Таблица истинности — таблица, в которой указаны значения логической функции для всех возможных комбинаций значений ее аргументов.
Запишем таблицы истинности для логических операций в соответствии с определениями, данными выше.
sites.google.com
Информатика Логика Законы

§ 3. Законы алгебры логики
Итак, мы познакомились с понятием логического выражения и увидели, каким образом его строить по высказыванию на русском языке. Следующий шаг – изучение преобразований логических выражений.
Логические выражения, зависящие от одних и тех же логических переменных, называются равносильными, если на любом наборе значений переменных они принимают одинаковое значение (`0` или `1`). В дальнейшем для обозначения равносильности логических выражений мы будем использовать знак равенства.
это некоторые стандартные преобразования логических выражений, при которых сохраняется равносильность. Начнём с самых простых законов:
1) Законы поглощения констант
2) Законы поглощения переменных
3) Законы идемпотентности
4) Закон двойного отрицания
5) Закон противоречия
6) Закон исключённого третьего
Приведённые законы ещё называют аксиомами алгебры логики. Истинность этих и всех последующих законов легко можно установить, построив таблицу истинности для левого и правого логического выражения.
Переходим к группе законов, которые практически аналогичны законам алгебры чисел.
7) Законы коммутативности
Здесь стоит сделать замечание, что помимо конъюнкции и дизъюнкции свойством коммутативности также обладают эквивалентность и строгая дизъюнкция. Импликация – единственная из изучаемых операций, которая имеет два операнда и не обладает свойством коммутативности.
8) Законы ассоциативности
(x & y) & z = x & (y & z),
(x`vv`y) `vv` z = x `vv` (y `vv` z);
9) Законы дистрибутивности
Первый из законов дистрибутивности аналогичен закону дистрибутивности в алгебре чисел, если конъюнкцию считать умножением, а дизъюнкцию – сложением. Второй же закон дистрибутивности отличается от алгебры чисел, поэтому рекомендуется обратить на него особое внимание и в дальнейшем использовать при решении задач на упрощение выражений.
Кроме аксиом и алгебраических свойств операций ещё существуют особые законы алгебры логики.
10) Законы де Моргана
`bar(x & y)= barx vv bary` ,
11) Загоны поглощения (не путать с аксиомами поглощения переменных нулём или единицей)
Рассмотрим пример доказательства первого закона де Моргана при помощи построения таблицы истинности.
Так как результирующие столбцы совпали, то выражения, стоящие в левой и правой частях закона, равносильны.
В алгебре при решении задач на упрощение выражений большой популярностью пользовалась операция вынесения общего множителя за скобки. В алгебре логики эта операция также является легитимной, благодаря законам дистрибутивности и закону поглощения константы `1`. Продемонстрируем этот приём на простом примере: докажем первый закон поглощения, не используя таблицу истинности.
Наше начальное выражение: x `vv` (x & y) . Выносим x за скобки и получаем следующее выражение:
x &(1 `vv` y) . Используем закон поглощения переменной константой `1` и получаем следующее выражение: x & 1. И теперь используем закон поглощения константы и получаем просто x .
В заключение, следует сказать несколько слов об операции импликации. Как уже отмечалось выше, импликация не обладает свойством коммутативности. Её операнды неравноправны, поэтому каждый из них имеет уникальное название. Левый операнд импликации называется посылкой, а правый – следствием. Из таблицы истинности импликации следует, что она истинна, когда истинно следствие, либо ложна посылка. Единственный случай, когда импликация ложна – это случай истинной посылки и ложного следствия. Таким образом, мы подошли к последнему закону алгебры логики, который бывает полезен при упрощении выражений.
12) Закон преобразования импликации
Необходимо ещё отметить, что в сложных логических выражениях у операций есть порядок приоритетов.
3) Дизъюнкция, строгая дизъюнкция, эквивалентность
zftsh.online
Смотрите так же:
xn--i1abbnckbmcl9fb.xn--p1ai
Информатика
Законы логики и правила преобразования логических выражений.
Изучаем основные законы логики, учимся преобразовывать логические выражения, используя логические законы, вводим понятие “нормальная форма логической формулы”, закрепляем навыки упрощения логических выражений, используя логические законы.

