Кто открыл закон о упругой деформации

Науколандия

Статьи по естественным наукам и математике

Сила упругости и закон Гука

Чем большей деформации подвергается тело, тем значительней в нем возникает сила упругости. Это значит, что деформация и сила упругости взаимосвязаны, и по изменению одной величины можно судить об изменении другой. Так, зная деформацию тела, можно вычислить возникающую в нем силу упругости. Или, зная силу упругости, определить степень деформации тела.

Если к пружине подвешивать разное количество гирек одинаковой массы, то чем больше их будет подвешено, тем сильнее пружина растянется, то есть деформируется. Чем больше растянута пружина, тем большая в ней возникает силы упругости. Причем опыт показывает, что каждая следующая подвешенная гирька увеличивает длину пружины на одну и туже величину.

Так, например, если исходная длина пружины была 5 см, а подвешивание на ней одной гирьки увеличило ее на 1 см (т. е. пружина стала длиной 6 см), то подвешивание двух гирек увеличит ее на 2 см (общая длина составит 7 см), а трех — на 3 см (длина пружины будет 8 см).

Еще до опыта известно, что вес и возникающая под его действием сила упругости находятся друг с другом в прямопропорциональной зависимости. Кратное увеличение веса во столько же раз увеличит силу упругости. Опыт же показывает, что деформация точно также зависит от веса: кратное увеличение веса во столько же раз увеличивает изменения в длине. Это значит, что, исключив вес, можно установить прямопропорциональную зависимость между силой упругости и деформацией.

Если обозначить удлинение пружины в результате ее растяжения как x или как ∆ l ( l ₁ – l ₀, где l ₀ — начальная длина, l ₁ — длина растянутой пружины), то зависимость силы упругости от растяжения можно выразить такой формулой:

В формуле используется коэффициент k . Он показывает, в какой именно зависимости находятся сила упругости и удлинение. Ведь удлинение на каждый сантиметр может увеличивать силу упругости одной пружины на 0,5 Н, второй на 1 Н, а третьей на 2 Н. Для первой пружины формула будет выглядеть как F_упр = 0,5x, для второй — F_упр = x, для третьей — F_упр = 2x.

Коэффициент k называют жесткостью пружины. Чем жестче пружина, тем труднее ее растянуть, и тем большее значение будет иметь k. А чем больше k, тем больше будет сила упругости (F_упр) при равных удлинения (x) разных пружин.

Жесткость зависит от материала, из которого изготовлена пружина, ее формы и размеров.

Единицей измерения жесткости является Н/м (ньютон на метр). Жесткость показывает, сколько ньютонов (сколько сил) надо приложить к пружине, чтобы растянуть ее на 1 м. Или насколько метров растянется пружина, если приложить для ее растяжения силу в 1 Н. Например, к пружине приложили силу в 1 Н, и она растянулась на 1 см (0,01 м). Это значит, что ее жесткость равна 1 Н / 0,01 м = 100 Н/м.

Также, если обратить внимание на единицы измерения, то станет понятно, почему жесткость измеряется в Н/м. Сила упругости, как и любая сила, измеряется в ньютонах, а расстояние — в метрах. Чтобы уровнять по единицам измерения левую и правую части уравнения F_упр = kx, надо в правой части сократить метры (то есть поделить на них) и добавить ньютоны (то есть умножить на них).

Соотношение между силой упругости и деформацией упругого тела, описываемое формулой F_упр = kx, открыл английский ученый Роберт Гук в 1660 году, поэтому это соотношение носит его имя и называется законом Гука.

Упругой деформацией является такая, когда после прекращения действия сил, тело возвращается в свое исходное состояние. Бывают тела, которые почти нельзя подвергнуть упругой деформации, а у других она может быть достаточно большой. Например, поставив тяжелый предмет на кусок мягкой глины, вы измените его форму, и этот кусок сам уже не вернется в исходное состояние. Однако если вы растяните резиновый жгут, то после того, как отпустите его, он вернет свои исходные размеры. Следует помнить, что закон Гука применим только для упругих деформаций.

Формула F_упр = kx дает возможность по известным двум величинам вычислять третью. Так, зная приложенную силу и удлинение, можно узнать жесткость тела. Зная, жесткость и удлинение, найти силу упругости. А зная силу упругости и жесткость, вычислить изменение длины.

scienceland.info

МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА

ОСНОВЫ МЕХАНИКИ СПЛОШНЫХ СРЕД

VI . ОСНОВЫ МЕХАНИКИ СПЛОШНЫХ СРЕД

6.1. Упругие и пластические деформации

Под действием приложенных сил все тела изменяют свою форму и объем, т.е. деформируются.

Для твердых тел различают деформации: упругие и пластические.

Упругими называют деформации , которые исчезают после прекращения действия сил, а тела восстанавливают свою форму и объем.

Пластическими называют деформации , которые сохраняются после прекращения действия сил, а тела не восстанавливают свою первоначальную форму и объем.

Пластическая деформация возникает при холодной обработке металлов: штамповке, ковке и т.д. Деформация будет упругой или пластической зависит не только от свойств материала тела, но и от величины приложенных сил. Тела, которые под действием любых сил испытывают только упругие деформации, называют идеально упругими. Для таких тел существует однозначная зависимость между действующими силами и вызываемыми ими упругими деформациями. Мы ограничимся изучением упругих деформациями, которые подчиняются закону Гука .

ГУК Роберт (18. VII 1635—ЗЛИ 1703) — английский физик, член Лон­донского королевского об-ва (с 1663 г.) и его секретарь (1677—1683 гг.). Учился в Оксфордском ун-те, где стал ассистентом Р. Бойля. Профессор Лондонского ун-та (с 1665 г.). Научные работы относятся к теплоте, упругости, оптике, небесной механике. Вместе с Р. Бойлем усовершенствовал (1659 г.) воздушный насос Герике, а с X . Гюйгенсом установил (около 1660 г.) постоянные точки термометра — точку таяния льда и точку кипения годы. В 1660 г. открыл закон упругости для твердых тел (закон Гука).

Усовершенствовал микроскоп, что позволило ему осуществить ряд микроскопических исследований, в частности наблюдать тонкие слои (мыльные пузыри, масляные пленки и т. п.) в световых пучков, изучать строение растений. Последнее привело его к открытию клеточного строения организмов. Он первый в работе «Микрография» (1665 г.), основываясь на собственных микроскопических исследованиях, описал клет­ки бузины, укропа, моркови и других растений, причем сам ввел термин «клетка». В «Микрографии» Гук также дает свою теорию цветов, окраску тонких слоев он объясняет сложением световых импульсов, отраженных от верхней и нижней поверхностей, распространение света от источни­ка сравнивает с распространением волн на воде от брошенного камня. Положил начало физической оптике. Гук был активным противником корпускулярной теории света И. Ньютона, возражал он и против того, что белый свет состоит из суммы простых цветов. В 1672 г. осуществил опыты по дифракции света, аналогичные опытам Ф. Гримальди, придер­живался волновой теории света, выдвинул гипотезу о поперечном ха­рактере световых волн.

В «Трактате о движении Земли» в 1674 г. высказал идею тяготения и дал свою систему мироздания. В 1680 г. Гук пришел к выводу, что сила тяготения обратно пропорциональна квадрату расстояния.

Изотропными называют тела , физические свойства которых по всем направлениям одинаковы.

Анизотропными называют тела , физические свойства которых различны по разным направлениям.

Приведенные определения являются относительными, так как реальные тела могут вести себя как изотропные по отношению к одним свойствам и как анизотропные — к другим. Например, кристаллы кубической системы ведут себя как изотропные, если в них распространяется свет, но они — анизотропны, если рассматривать их упругие свойства. В дальнейшем ограничимся исследованием изотропных тел.

Наиболее широкое распространение в природе имеют металлы с поликристаллической структурой, т.е. состоящие из множества мельчайших произвольно ориентированных кристаллов. В результате пластической деформации хаотичность в ориентации кристаллов может нарушиться и, после прекращения действия сил, вещество будет анизотропным, что наблюдается, например, при вытягивании и кручении проволоки.

Силу, отнесенную к единице площади поверхности, на которую они действуют, называют механическим напряжением s _n .

Если напряжение не превосходит предела упругости, то деформация будет упругой.

Предельные напряжения приложенные к телу, после действия которых оно еще сохраняет свои упругие свойства, называют пределом упругости.

Различают напряжения сжатия, растяжения, изгиба, кручения и т.д. Если под действием сил, приложенных к телу (стержню), оно растягивается, то возникающие напряжения называют натяжением

Если стержень сжать, то возникающие напряжения называют давлением:

Если ℓ ₀ — длина недеформированного стержня, то после приложения силы он получает удлинение Δℓ .

Тогда длина стержня

Отношение Δ ℓ к ℓ ₀ , называют относительным удлинением, т.е.

На основании опытов, Гуком установлен закон: в пределах упругости напряжение (давление) пропорционально относительному удлинению (сжатию), т.е.

ЮНГ Томас (13. VI 1773 — 10. V 1829) — английский ученый, один из создателей волновой теории света. Р. в Милвертоне. С ранних лет обнаружил необыкновенные способности и феноменальную память. В 2 года научился бегло читать, а в 4 знал на память много сочинений английских по­этов; в 8—9 лет овладел токарным ремеслом и мастерил различные физические приборы, к 14 годам познакомился с дифференциальным исчислением (по Ньютону), изучил много языков (греческий, латынь, французский, итальянский, арабский и др.). Учился в Лондонском, Эдинбургском и Гёттингенском ун-тах, где сначала изучал медицину, но потом увлекся физикой, в частности оптикой и акустикой. В 1801 —1804 гг. — профессор Королевского ин-та, с 1811 г. — врач в больнице Св. Георгия (Лондон), одновременно с 1818 г. — секретарь Бюро долгот, руководил изданием «Морского календаря», был секретарем Лондонского королевского об-ва. В пос­ледние годы жизни занимался составлением египетского словаря. Работы относятся к различным отраслям науки — оптике, аку­стике, теплоте, механике, математике, астрономии, геофизике, фило­логии, зоологии и др. Однако в истории науки наиболее известен как физик. Объяснил (1793 г.) явление аккомодации глаза изменением кри­визны хрусталика. В трактате «Опыты и проблемы относительно звука и света» (1800 г.) выступил в защиту волновой теории света, подверг критике корпускулярную теорию Ньютона; тут же впервые указал на усиление и ослабление звука при наложении звуковых волн. В 1801 г. первый объяснил явление интерференции света и ввел тер­мин «интерференция», в частности, исходя из своего принципа интер­ференции, объяснил кольца Ньютона. Выполнил также первый демон­страционный эксперимент по наблюдению интерференции света, полу­чив два когерентных источника света. Этот опыт стал классическим, как и известный опыт Френеля. В 1803 г. Юнг сделал попытку объяс­нить дифракцию света от тонкой нити, связывая ее с интерференцией, открыл интерференцию ультрафиолетовых лучей, показал, что при отражении луча света от более плотной среды происходит потеря полу­волны. Разрабатывал также теорию цветного зрения. В теории упругости Юнгу принадлежат исследования деформации сдвига, в 1807 г. он ввел характеристику упругости — модуль Юнга.

Соотношения (6.6) и (6.7) справедливы для любого твердого тела, но до определенного предела. На рис. 6.1 приведен график зависимости удлинения от величины приложенной силы.

До точки А (предел упругости) после прекращения действия силы длина стержня возвращается к первоначальной (область упругой деформации). За пределами упругости деформация становится частично или полностью необратимой (пластические деформации). Для большинства твердых тел линейность сохраняется почти до предела упругости. Если тело продолжать растягивать, то оно разрушится. Максимальную силу, которую нужно приложить к телу, не разрушая его, называют пределом прочности (т. Б, рис. 6.1).

Рассмотрим произвольную сплошную среду. Пусть она разделена на части 1 и 2 вдоль поверхности А-а-Б-б (рис. 6.2). Если тело деформировано, тогда его части взаимодействуют между собой по поверхности раздела, вдоль которой они граничат.

Для определения возникающих напряжений кроме сил, действующих в сечении А-а-Б-б, нужно знать, как эти силы распределены по сечению. Обозначим через dF силу, с которой тело 2 действует на тело 1 на бесконечно малой площадке dS . Тогда напряжение в соответствующей точке на границе сечения тела 1

где — единичный вектор нормали к площадке dS .

Напряжение s _{— n} в той же точке на границе сечения тела 2, такое же по величине, по противоположное по направлению, т.е.

Для определения механического напряжения в среде, на противоположно ориентированной площадке, в какой-либо ее точке, достаточно задать напряжения на трех взаимно перпендикулярных площадках: S_x , S_y , S_z , проходящих через эту точку, например, т. О (рис. 6.3). Это положение справедливо для покоящейся среды или движущейся с произвольным ускорением. В этом случае

S — площадь грани АВС; n — внешняя нормаль к ней.

Следовательно, напряжение в каждой точке упруго деформированного тела можно характеризовать тремя векторами или девятью их проекциями на оси координат Х, У, Z :

которые называют тензором упругих напряжений.

files.lib.sfu-kras.ru

Кто открыл закон о упругой деформации

1.12. Сила упругости. Закон Гука

При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости .

Простейшим видом деформации являются деформации растяжения и сжатия (рис. 1.12.1).

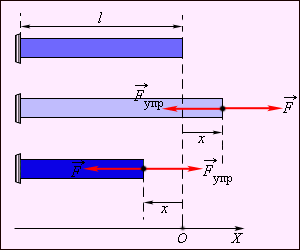
Закон Гука может быть обобщен и на случай более сложных деформаций. Например, при деформации изгиба упругая сила пропорциональна прогибу стержня, концы которого лежат на двух опорах (рис. 1.12.2).

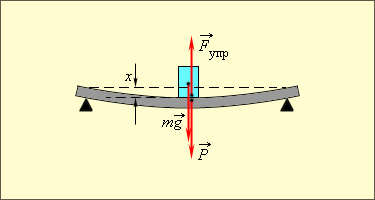
Упругую силу 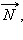действующую на тело со стороны опоры (или подвеса), называют силой реакции опоры . При соприкосновении тел сила реакции опоры направлена перпендикулярно поверхности соприкосновения. Поэтому ее часто называют силой нормального давления . Если тело лежит на горизонтальном неподвижном столе, сила реакции опоры направлена вертикально вверх и уравновешивает силу тяжести: 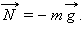Сила 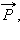с которой тело действует на стол, называется весом тела.

В технике часто применяются спиралеобразные пружины (рис. 1.12.3). При растяжении или сжатии пружин возникают упругие силы, которые также подчиняются закону Гука. Коэффициент k называют жесткостью пружины . В пределах применимости закона Гука пружины способны сильно изменять свою длину. Поэтому их часто используют для измерения сил. Пружину, растяжение которой проградуировано в единицах силы, называют динамометром . Следует иметь в виду, что при растяжении или сжатии пружины в ее витках возникают сложные деформации кручения и изгиба.

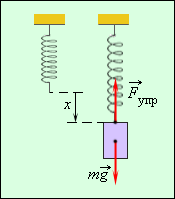
В отличие от пружин и некоторых эластичных материалов (резина) деформация растяжения или сжатия упругих стержней (или проволок) подчиняются линейному закону Гука в очень узких пределах. Для металлов относительная деформация ε = x / l не должна превышать 1 % . При больших деформациях возникают необратимые явления (текучесть) и разрушение материала.

physics.ru

Занимательные факты по физике по теме:
Сила упругости и другое.

Знание законов физики помогает сделать нашу жизнь не только более удобной , но и позволяет совершать » поразительные эффекты» в искусстве, в частности цирковом.

Предварительный просмотр:

В 1660 году в возрасте 25 лет английский учёный Роберт Гук открыл закон пропорциональности между силой, приложенной к упругому телу, и его деформацией ( в последствии закон Гука ).

где — жёсткость тела, — величина деформации .

В словесной формулировке закон Гука звучит следующим образом:

Сила упругости, возникающая при деформации тела, прямо пропорциональна удлинению тела и направлена противоположно направлению перемещения частиц тела относительно других частиц при деформации.

Этот закон нашёл применение почти во всех областях нашей жизни: в строительстве, в архитектуре, в торговле, в автомобилестроении. Сила упругости так же нашла своё применение и в цирке при демонстрации номера « Живые снаряды». В этом номере своё применение нашли и многие другие разделы физики. А теперь более подробно.

Стрельба из пушки «живым снарядом» была впервые показана в конце 80-х годов позапрошлого века в знаменитом парижском цирке Франкони. Номер назывался «Человек- бомба». Посредине арены устанавливали большую пушку. Команда заряжала ее «человеком-снарядом». Роль его выполняла артистка мисс Люлю. Очевидец аттракциона рассказывал: «Музыка стихала, наступал момент тоскливого молчания. Наконец, слышалась отрывистая команда: «Пли!», и под гром выстрела, среди огня и дыма из пушки вылетала «живая бомба». Эффект был поразительный».

Зрители не подозревали, что на самом деле артистку выбрасывали из пушки не пороховые газы, а – мощная упругая пружина, помещавшаяся в стволе. Грохот выстрела, дым и огонь служили целям усиления эффекта. Долгое время у бесстрашной мисс Люлю не находилось последователей, но с течением времени выступления ее постепенно забылись, и когда осенью 1927 года в Советский Союз прибыл с аттракционом «Человек-снаряд» итальянец Уго Цаккини, его гастроли подавались как мировая сенсация. Афиши возвещали: «Впервые в Европе! Невиданный аттракцион!»

Цаккини выступал в Москве и Ленинграде. Орудие его имело ствол длиной около пяти метров и диаметром сантиметров шестьдесят. Внутри ствола скользил поршень. Цаккини — молодой человек, одетый в белый комбинезон, — влезал в ствол пушки через жерло, ногами к поршню. В момент выстрела сжатый воздух толкал поршень, и тот, стремительно двигаясь вперед, выбрасывал артиста из ствола. Смельчак пролетал по дуге и падал в сетку, натянутую над ареной. Цаккини взлетал вверх метров на пятнадцать. Но говорили, что он собирается увеличить высоту полета до пятидесяти метров и даже больше — до ста пятидесяти, хотя это и грозило очень большими перегрузками.

Цаккини еще выступал на аренах советских цирков, когда в нашу страну приехал другой иностранный гастролер, норвежский цирковой артист Лейнерт с партнерами. Лейнерт выступал везде, кроме Москвы, в Ленинграде, Казани, Туле, Одессе, Ростове, Харькове. И мало кто знал, что в Харьковском цирке за выступлениями норвежца внимательно наблюдал студент автомобильного института, 20-летний Семен Речицкий. Он приходил в цирк почти ежедневно. Дело в том, что Речицкий тоже решил создать подобный аттракцион, однако не просто его повторить, а превзойти.

Это решение пришло не случайно. Будучи опытным автомехаником, Семен Речицкий, кроме того, выступал в качестве акробата в самодеятельных эстрадных бригадах. Нашлись у него и помощники в создании «цирковой» пушки, включая техников Харьковского авиационного завода. Почти семиметровый ствол пушки размещался на шасси грузового автомобиля. Но для выбрасывания «живого снаряда» вместо силы упругости пружины или сжатого воздуха использовалась энергия тяжелого маховика весом 200 килограммов. Для его раскручивания применялся бензиновый двигатель. Сооружение весом около восьми тонн оказалось слишком громоздким и поэтому больше подходило для демонстрации в городских парках отдыха или на стадионах. Но зато и стреляла пушка дальше иностранных. Наконец, пушку Речицкого впервые увидела публика. Было это на харьковском стадионе «Динамо». Первым ее испытателем стал сам конструктор. Выброшенный из орудия, он пролетел по огромной дуге полтора десятка метров и упал невредимым в сеть, туго натянутую ряды». над землей. Вторым так же успешно «выстрелился» акробат Любимов. Можно было отправляться на гастроли по стране. В Москве аттракцион демонстрировали в парке имени М. Горького, а также в парке «Сокольники».В роли «живого снаряда» обычно выступала молодая гимнастка Вера Буслаева. Ствол пушки сначала устанавливался в горизонтальное положение. Исполнительница становилась на него. Ствол начинал медленно подниматься, а смелая гимнастка так же медленно шла по нему к жерлу. Затем она опускалась в ствол, стоявший уже наклонно дулом вверх. И вот запускался мотор. Маховик раскручивался. Речицкий, сидевший за пультом управления, поворачивал рычаг, могучая энергия стремительно вращавшегося маховика приводила в действие механизм пушки и тот выбрасывал артистку из ствола. Дальше — свободный полет и падение в спасительную сетку. При выстреле вес девушки увеличивался более чем в три раза, а при падении в сетку — раз в 14!

После Москвы пушку повезли в другие города. В июле 1936 года чудо-номер демонстрировался в Таганроге, из Таганрога отправились в Туркмению, в Красноводск.

Речицкий воевал во время Великой Отечественной войны и погиб в одном из боев. Идея аттракциона с пушкой между тем продолжала интересовать изобретательных и отчаянных людей. В конце 80-х годов прошлого века в роли «живого снаряда» выступил американец Дэвид Смит, бывший школьный учитель. По его словам, он покинул школу, поскольку не мог выдержать гвалта и выходок своих учеников. Пушку Смит сконструировал сам. Устройство ее всегда держал в секрете. Это была замечательная пушка. Она выстреливала своего создателя со скоростью до 80 километров в час! Пролетев над стадионом метров четыреста, Дэвид Смит пикировал вниз головой в нейлоновую сеть. Когда его спрашивали, не страшно ли ему залезать в дуло пушки, Смит отвечал: «Конечно, страшно. Но в этот момент я вспоминаю школу, своих сорванцов-учеников и радуюсь, что наконец-то нашел работу, подходящую для моих нервов».

nsportal.ru

История открытия закона Гука (сила упругости) Помогите пожалуйста срочно.

Зако́н Гу́ка — уравнение теории упругости, связывающее напряжение и деформацию упругой среды. Открыт в 1660 году английским учёным Робертом Гуком (Хуком) (англ. Robert Hooke). Поскольку закон Гука записывается для малых напряжений и деформаций, он имеет вид простой пропорциональности.

Для тонкого растяжимого стержня закон Гука имеет вид: . Здесь сила натяжения стержня, — его удлинение, а называется коэффициентом упругости (или жёсткостью) .

Очевидно, что коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Полезно выделить зависимость от размеров стержня (площади поперечного сечения и длины ) явно, записав коэффициент упругости как . Величина называется модулем Юнга и зависит только от свойств материала. Полезно теперь ввести относительное удлинение и нормальное напряжение в поперечном сечении . В этих обозначениях закон Гука записывается как . Величину, обратную жёсткости, называют податливостью.
[править]
Обобщённый закон Гука

В общем случае напряжения и деформации являются тензорами второго ранга в трёхмерном пространстве (имеют по 9 компонентов) . Связывающий их тензор упругих постоянных является тензором четвёртого ранга и содержит 81 коэффициент. Вследствие симметрии тензора, а также тензоров напряжений и деформаций, независимыми являются только 21 постоянная. Закон Гука выглядит следующим образом:

Для изотропного материала тензор содержит только два независимых коэффициента.

Следует иметь в виду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.
Представьте, что вы взялись за один конец упругой пружины, другой конец которой закреплен неподвижно, и принялись ее растягивать или сжимать. Чем больше вы сдавливаете пружину или растягиваете ее, тем сильнее она этому сопротивляется. Именно по такому принципу устроены любые пружинные весы — будь то безмен (в нем пружина растягивается) или платформенные пружинные весы (пружина сжимается) . В любом случае пружина противодействует деформации под воздействием веса груза, и сила гравитационного притяжения взвешиваемой массы к Земле уравновешивается силой упругости пружины. Благодаря этому мы можем измерять массу взвешиваемого объекта по отклонению конца пружины от ее нормального положения.

Первое по-настоящему научное исследование процесса упругого растяжения и сжатия вещества предпринял Роберт Гук. Первоначально в своем опыте он использовал даже не пружину, а струну, измеряя, насколько она удлиняется под воздействием различных сил, приложенных к одному ее концу, в то время как другой конец жестко закреплен. Ему удалось выяснить, что до определенного предела струна растягивается строго пропорционально величине приложенной силы, пока не достигает предела упругого растяжения (эластичности) и не начинает подвергаться необратимой нелинейной деформации (см. ниже) . В виде уравнения закон Гука записывается в следующей форме:

где F — сила упругого сопротивления струны, x — линейное растяжение или сжатие, а k — так называемый коэффициент упругости. Чем выше k, тем жестче струна и тем тяжелее она поддается растяжению или сжатию. Знак минус в формуле указывает на то, что струна противодействует деформации: при растяжении стремится укоротиться, а при сжатии — распрямиться.

otvet.mail.ru