Первый закон гиббса-коновалова

Законы Коновалова устанавливают связи между изменениями состава, давления и температуры в двойных двухфазных системах, они лежат в основе теории перегонки и ректификации бинарных смесей. Законы были обоснованы Коноваловым [19] путем оригинального, строго термодинамического рассмотрения.

Законы Коновалова непосредственно следуют из дифференциального уравнения Ван-дер-Ваальса.

Первый закон Коновалова формулируется так:

давление пара раствора возрастает (уменьшается) при увеличении концентрации того компонента, содержание которого в паре больше (меньше), чем в растворе; температура кипения раствора возрастает (уменьшается) при увеличении концентрации того компонента, содержание которого в паре меньше (больше), чем в растворе.

Из уравнения Ван-дер-Ваальса, записанного для жидкой и паровой фаз (II 1.23) и (II 1.24), получим соответствующие производные:

В этих уравнениях вторые производные энергии Гиббса по составу положительны в силу условий устойчивости, знаки объемных

и тепловых эффектов конденсации и испарения в обычных условиях вполне определенны, а именно:

Следовательно, знаки производных в (II 1.25)-(II 1.28) определяются знаками разности концентраций компонента в жидкости и паре:

Соотношения (111.30) представляют собою формулировку первого закона Коновалова для изотермических условий, (III.31) — для изобарных. Эти соотношения могут быть нарушены в том случае, если не выполнены условия (II 1.29), что для систем жидкость — пар возможно вблизи критических состояний.

Второй закон Коновалова формулируется так:

если давление и температура сосуществования двух бинарных фаз имеют экстремум (максимум или минимум), то составы фаз одинаковы.

Это утверждение справедливо для фаз любой природы. В случае систем жидкость — пар второй закон Коновалова определяет основное свойство азеотропов. Он сразу же следует из уравнения (II 1.25)-(II 1.28), так как очевидно, что только при условии равенства составов жидкости и пара производные левой части уравнений могут иметь нулевые значения.

Положение о симбатности изменений составов раствора и пара в изотермических или изобарных условиях называют третьим законом Коновалова (иногда это положение определяют как следствие первого закона). Действительно, из сопоставления уравнений (II 1.25) с (111.26) и (111.27) с (111.28) сразу же получаем:

Рис. 111.5. (см. скан) Типы (а-в) диаграмм равновесия жидкость—пар в двойных системах

В этих соотношениях значения вторых производных энергии Гиббса по составу положительны в силу условий устойчивости, знаки же и как и знаки и различны по физическому смыслу величин. Это и определяет знак неравенств.

Симбатность изменений состава раствора и пара может быть нарушена в области, близкой к критическому состоянию системы.

Соотношения (III.32) и (III.33) определяют вид диаграмм

На рис. III.5 схематически изображены три основных типа диаграмм равновесия, жидкость — пар в бинарных системах, в которых расслаивание жидкости отсутствует. Диаграммы построены в координатах они наглядно иллюстрируют выполнение всех законов Коновалова. Для диаграмм типа а следует оговорить, что через х и у выражена концентрация более летучего компонента.

know.alnam.ru

Справочник химика 21

Химия и химическая технология

Коновалова закон

Гнббса-Дюгема уравнение 1/1064.127, 1014,1065 3/886 4/366, 373 5/500 Гиббса-Коновалова закон 2/899 Гиббса-Кюри условие 2/318 Гиббса-Кюри-Вульфа принцип. 1/1172, 1173 Гиббса-Плато канал 4/1206, 1207 Гиббса-Розебома треугольник 3/188 ГНббса-Смита условие 4/1206 Гиббса-Томсона эффект 2/319 Гиббса-Фольмера теория 2/317, 318 Гиббсит 1/211, 213 [c.578]

А. Равновесия пар — жидкий раствор в системах с неограниченной взаимной растворимостью жидкостей. Законы Гиббса— Коновалова. Законы Вревского. Перегонка жидких смесей. Если раствор образован из двух летучих жидкостей, то пар, находящийся в равновесии с жидким раствором, будет содержать оба компонента. В общем случае состав пара отличается от состава жидкого раствора, из которого он получен. Состав паровой фазы легко установить, зная состав жидкой фазы, если пар, представляющий смесь идеальных газов, находится в равновесии с идеальным раствором. Исходя из соотношений [c.388]

Законы Гиббса—Коновалова. Законы Гиббса — Коновалова характеризуют изменение свойств систем при изобарических и изотермических процессах. [c.230]

Взаимное положение кривых на фазовых диаграммах I — х — у м у — X как для идеальных, так и для реальных систем могут быть определены С помощью законов Коновалова. Законы Коновалова [c.104]

Если законы Коновалова характеризуют изменение состояния равновесия двухкомпонентных двухфазных систем при изобарных или изотермических условиях, то законы (правила) Вревского определяют закономерности влияния на фазовые равновесия бинарных систем изменений температуры и давления при наложении определенных условий на изменения составов равновесных фаз. Как и законы Коновалова, законы Вревского [201 лежат в основе термодинамической теории равновесия жидкость — пар и составляют классическое наследие Ленинградской физикохимической школы. [c.40]

Второй закон Коновалова (закон Гиббса—Коновалова), утверждающий равенство составов сосуществующих фаз при условиях экстремума температуры и давления, применим к двухфазным системам любой природы и с любым числом компонентов, это положение известно давно. [c.85]

Конифериловый спирт 893, 958, 961 Коновалова законы 893, 66, 57 Коновалова реакция 694 Конопляное масло — см. Жиры растительные [c.534]

Реальные жидкие Р. в общем случае не подчиняются законам идеальных концентрированных Р. В частности они показывают отклонения от закона Рауля. Если парциальные давления паров компопентов больше вычисленных по закону Рауля, то отклонения наз. положительными, если меньше, то — отрицательными. В первом случае на кривой зависимости общего давления пара от состава Р. может появиться максимум, во втором — минимум (подробнее см. Жидкие системы и Коновалова законы). В точке максимума или минимума состав жидкой смеси одинаков с составом равновесного с ней пара. Такая смесь наз. азеотропной (см. Азеотропные смеси). [c.258]

В отличие от законов Коновалова законы Вревского описывают изменения составов фаз систем при условии постоянства состава одной из сосуществующих фаз. [c.64]

Двухкомпоиеншые системы. Кривые зависимости общего давления от состава при постоянной т-ре (изотермы общего давления) имеют максимумы или минимумы (точки А А.2, Аз на рис, 1). Соответственно на изобарах т-р кипения в этих точках имеются минимумы или максимумы (см. Коновалова законы). При максимуме на изотерме (минимуме на изобаре) азеотроп наз. положительным, при минимуме на изотерме (максимуме на изобаре)-отрицательным. Среди двойных систем с A. . примерно 93% приходится на системы с положит, азеотропами. Известны случаи существования в одной системе двух азеотропов разного знака при S-образной изобаре т-р кипения (напр., в системе фторбензол-бензол). [c.45]

Исторический очерк. Осн. идея Ф.-х. а. была высказана М.В. Ломоносовым (1752), первые попытки установить образование в системе хим. соед., исходя из зависимости ее св- от состава, относятся к нач. 19 в. В сер. 19 в. работами П.П. Аносова (1831), Г.К. Сорби (1864), Д.К. Чернова (1869) были заложены основы металловедения Д.И. Менделеевым впервые был проведен геом. анализ диафамм состав — св-во на примере имения гидратов серной к-ты. К этому же периоду относятся работы В.Ф. Алексеева о взаимной р-ри-мости жидкостей, Д.П. Коновалова — об упругости пара р-ров (см. Коновалова законы), И.Ф. Шредера — о температурной зависимости р-римости (см. Растворимость). На рубеже 19-20 вв. в связи с потребностями техники началось бурное развитие Ф.-х. а. (А. Ле Шателье, Я. Вант Гофф, Ф. Осмовд, У. Робертс-Остен, Я. Ван Лаар и др.). Основополагающие теоретич. и эксперим. работы совр. Ф.-х. а. принадлежат [c.92]

Конкурентные ингибиторы 2/434 Конкурирующие реакции, метод 2/897, 754, 898, 1295 Конноды 2/58, 61, 63 Коновалова законы 2/899 1/66 5/176 Коновалова реакция 2/899, 314, 900 [c.629]

Р. п. аналогичны Коновалова законам, установленным для двойных жидких систем, находяшйхся в равновесии с паром. Розебом показал, что для двойных систем с непрерывным рядом твердых р-ров существует 3 основных типа концентрационно-температурных диаграмм (рис.), аналогичных установленным трем типам диаграмм температура кипения — концентрация для двойных жидких систем. Для твердых р-ров типа [c.349]

Смотреть страницы где упоминается термин Коновалова закон: [c.565] [c.347] [c.529] [c.347] Физическая химия (1980) — [ c.0 ]

Процессы и аппараты химической технологии Часть 2 (2002) — [ c.104 ]

Краткий курс физической химии Изд5 (1978) — [ c.311 , c.313 ]

Основы техники кристаллизации расплавов (1975) — [ c.24 ]

Курс физической химии Том 1 Издание 2 (1969) — [ c.182 , c.188 ]

Курс физической химии Том 1 Издание 2 (копия) (1970) — [ c.182 , c.188 ]

Процессы и аппараты химической технологии Часть 2 (1995) — [ c.104 ]

chem21.info

Законы Гиббса-Коновалова;

Законы Гиббса-Коновалова (1881 г.) установливают соотношения между составами равновесных жидких растворов и составами их паров, а также общим давлением насыщенного пара над ними.

Первый закон Гиббса-Коновалова гласит: в насыщенном паре над раствором преобладает по сравнению с раствором тот компонент, добавление которого к раствору приводит к возрастанию общего давления насыщенного пара (пар обогащен легколетучим компонентом). Данный закон выполняется для любых растворов, а на рассматриваемом явлении основана фракционная перегонка (ректификация), позволяющая разделить смесь взаимно-растворимых жидкостей.

Докажем первый закон Гиббса-Коновалова, для чего воспользуемся уравнением Дюгема-Маргулеса (8.10), устанавливающим связь между изменениями парциальных давлений пара компонентов и составом раствора при постоянных температуре и давлении. В расчете на 1 моль жидкого бинарного раствора указанное уравнение принимает вид

.

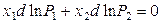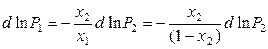. (8.35)

Преобразуем уравнение (8.35):

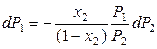. (8.36)

, ,

. (8.37)

, ,

. (8.38)

Разделим правую и левую части уравнения (8.38) на dx₂, получим:

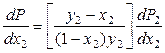. (8.39)

Поскольку производная (dP₂/dx₂) > 0 (парциальное давление второго компонента в паре увеличивается с ростом его мольной доли в растворе), то знак производной (dP/dx₂) определяется знаком разности (y₂ – x₂). Если y₂ > x₂, то (dP/dx₂) > 0, что и требовалось доказать.

С учетом вышеизложенного первый закон Гиббса-Коновалова может быть сформулирован и так: общее давление пара над раствором растёт с ростом доли в растворе того компонента, который богаче представлен в паре (более летучего компонента).

Второй закон Гиббса-Коновалова касается более частных случаев и выполняется для реальных растворов с большими отклонениями от закона Рауля, на кривых «общее давление пара – состав» для которых имеются минимумы или максимумы. Второй закон Гиббса-Коновалова гласит: максимум на кривой общего давления соответствует минимуму на кривой температур кипения и отвечает такому равновесию раствора и насыщенного пара, при котором составы фаз одинаковы, и наоборот.

Экстремумы на кривой зависимости общего давления насыщенного пара от состава раствора удовлетворяют условию (dP/dx₂) = 0, а в соответствии с уравнением (8.39) это возможно, только если в этих точках y₂ = x₂. Итак, в экстремумах общего давления пара (или температур кипения) раствор и насыщенный пар имеют одинаковый состав.

Возможные диаграммы состояния бинарных систем с максимумом на кривой давления пара и минимумом на кривой температур кипения представлены на рис. 8.7.

Рис. 8.7. Диаграммы состояния бинарных систем с максимумом на кривой давления пара (а) и минимумом на кривой температур кипения (б).

Смеси, у которых раствор и пар одинаковы по составу, называются азеотропными, или нераздельнокипящими. Путём перегонки азеотропные растворы не разделяются (составы фаз равны). Но их можно разделить следующими методами:

— путём химического связывания одного из компонентов;

— путем добавления в систему третьего компонента;

— путем ректификации на двух последовательных колонках при различных давлениях.

Примерами азеотропных смесей с минимумами на кривых температур кипения являются растворы, содержащие Н₂О и С₂Н₅ОН (96,5%), метанол и ацетон. Примерами азеотропных смесей с максимумами на кривых кипения являются растворы, содержащие Н₂О и НСl (20%), ацетон и хлороформ.

Третий закон Гиббса-Коновалова гласит: в изотермических или изобарических условиях состав насыщенного пара и состав жидкого раствора меняются синбатно (составы обеих фаз меняются в одном направлении). Данный закон логично следует из изученного материала и для его обоснования достаточно еще раз внимательно изучить диаграммы состояния, представленные, например, на рис. 8.3 – 8.5.

studopedia.su

Первый закон гиббса-коновалова

Кафедра физической и коллоидной химии ЮФУ

Материалы к лекциям для студентов химфака

Состав равновесного пара над раствором

Если рассмотреть, как соотносятся состав раствора и состав равновесного пара, то нетрудно показать, что в общем случае мольная доля компонента в растворе Х_i не совпадает с мольной долей компонента в паре Y_i.

(10)

Подставив сюда уравнение (9), получаем:

(11)

Разделив числитель и знаменатель правой части уравнения на Р°_А и введя обозначение , получим:

(12)

Из уравнения (12) видно, что Y_B = X_B только при условии, что α = 1, т.е. при равенстве давлений насыщенного пара чистых компонентов А и В. Если α > 1, то мольная доля компонента В в паре оказывается больше, чем его мольная доля в растворе (и наоборот). Вид зависимости состава равновесного пара от состава раствора приведён на рисунке 3.

Рис. 3. Зависимость состава пара от состава раствора для идеальных растворов.

Данную зависимость состава пара от состава раствора качественно описывает первый закон Коновалова :

Равновесный пар по сравнению с жидкостью относительно обогащён тем компонентом, добавление которого к жидкости повышает общее давление пара над раствором (или, что то же самое, понижает температуру кипения раствора при некотором постоянном давлении).

Первый закон Коновалова применим как к идеальным, так и к неидеальным растворам. Если отклонения от первого закона Рауля невелики, то зависимость состава пара от состава раствора имеет вид, аналогичный изображённому на рисунке 3 для случая, когда α > 1. Если отклонения раствора от идеального велики, на кривой зависимости общего давления пара от состава раствора может появиться экстремум (максимум или минимум для положительных и отрицательных отклонений соответственно). В этом случае зависимость состава пара от состава раствора имеет более сложный вид, показанный на рисунке 4.

Рис. 4. Зависимость состава пара от состава раствора для систем, имеющих экстремум на кривой зависимости общего давления пара от состава раствора.

Аналогичная ситуация может иметь место и для близких к идеальному раствору систем, в которых компоненты раствора имеют близкие температуры кипения (давления насыщенного пара над чистым компонентом). Данная ситуация описывается вторым законом Коновалова :

Точки экстремума на кривой зависимости общего давления пара от состава раствора отвечают растворам, состав равновесного пара над которыми совпадает с составом раствора.

Такие растворы называются нераздельно кипящими или азеотропными смесями .

Законы Коновалова можно вывести термодинамически, воспользовавшись уравнением Дюгема – Моргулиса , связывающим парциальные давления паров компонентов бинарного раствора с их мольными долями в растворе:

(13)

Переписав уравнение (13) в виде

(14)

и подставив туда X_A = 1 – X_B, получаем:

=> (15)

Выражая dP_A из уравнения (15) и подставляя вместо парциального давления каждого из компонентов произведение общего давления пара на мольную долю компонента в паре (P_A = PY_A = P(1–Y_B), P_B = PY_B), получим:

(16)

Учитывая, что, согласно закону Дальтона, dP = dP_A + dP_B, уравнение (16) можно переписать относительно dP:

(17)

Разделив это выражение на dX_B, получаем зависимость, связывающую общее давление пара над бинарным раствором с мольной долей компонента B в растворе:

(18)

Таким образом, если добавление в раствор компонента B увеличивает общее давление пара ( > 0), то, поскольку производная всегда положительна, получаем, что Y_B – X_B > 0, доказав 1-й закон Коновалова.

В точке экстремума производная давления по мольной доле B равна нулю. Отсюда получаем:

=> => (19)

На различии составов раствора и равновесного с ним пара основано разделение растворов с помощью перегонки. Для рассмотрения равновесия в таких системах удобно пользоваться диаграммами состояния раствор – пар в координатах давление пара – состав или температура кипения – состав.

Copyright © С. И. Левченков, 2005.

www.physchem.chimfak.rsu.ru

Законы Коновалова.

На практике возникает необходимость не только перевести вещества в растворенное состояние, но и разделить жидкие растворы на составляющие их компоненты.

Наиболее распространенные методы разделения жидких однородных растворов, состоящих из летучих компонентов – это перегонка и ректификация. Их широко применяют в промышленности. Теоретической основой процесса разделения жидких растворов, состоящих из летучих компонентов, являются законы Коновалова (или Гиббса – Коновалова).

Законы Коновалова устанавливают связь между составом жидкого раствора смеси летучих компонентов и составом насыщенного равновесного с ним пара в зависимости от температуры и давления.

В равновесной двухкомпонентной системе сумма мольных долей компонентов в жидкой (N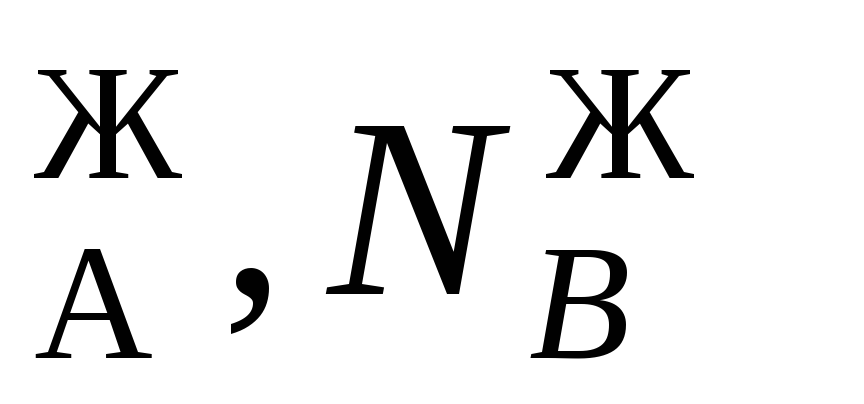) и паровой (N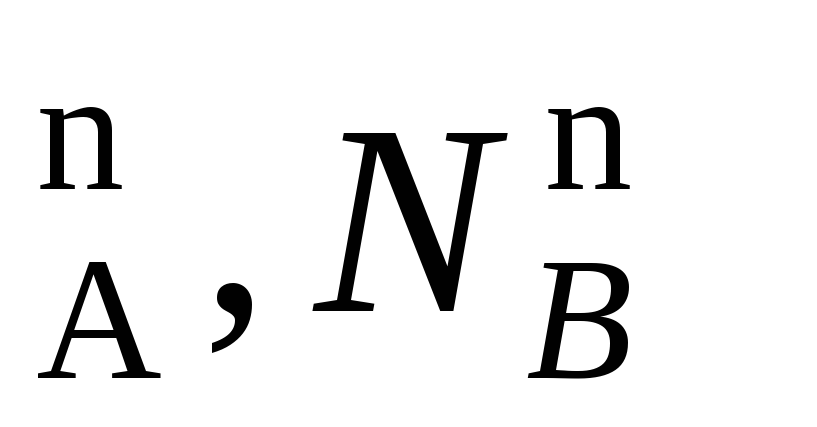) фазах равна единице, т.е.

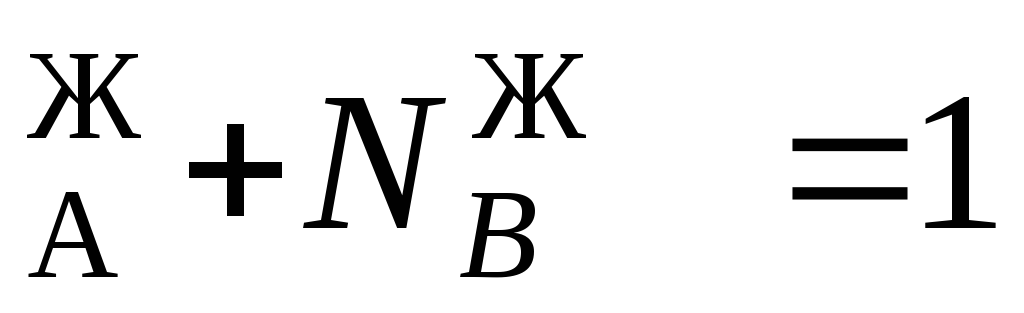N;N(*)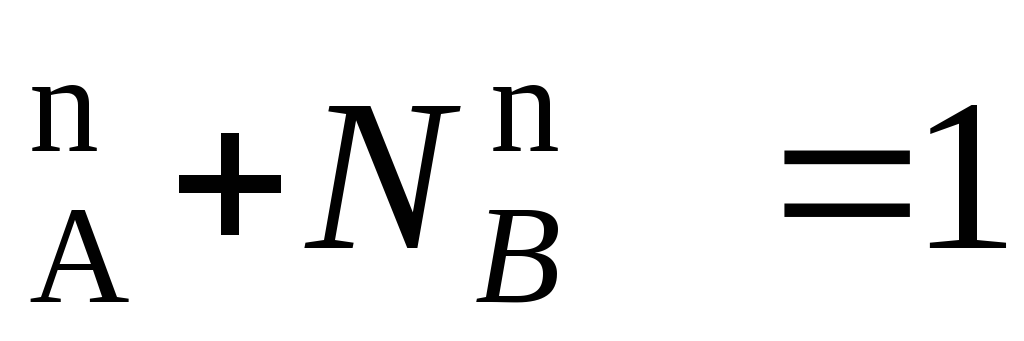

Подчеркнем, что эти условия и весь ход дальнейших рассуждений справедливы для жидких растворов двух летучих компонентов, причем пар, находящихся в равновесии с жидким раствором, содержит оба компонента. Летучим компонентомназывают жидкость, которая при данной температуре имеет достаточно высокое давление пара. К числу жидких растворов из летучих компонентов относятся продукты перегонки нефти (бензин, керосин и др.).

Условия (*) не означают, что составы жидкости и находящегося в равновесии с ней пора совпадают, т.е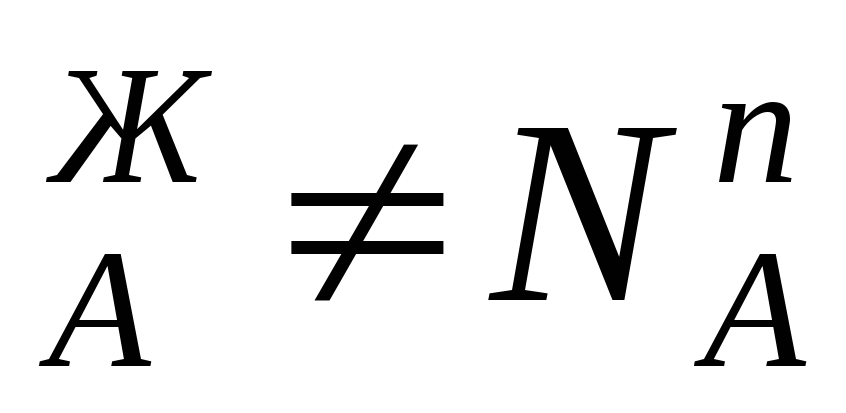. NиN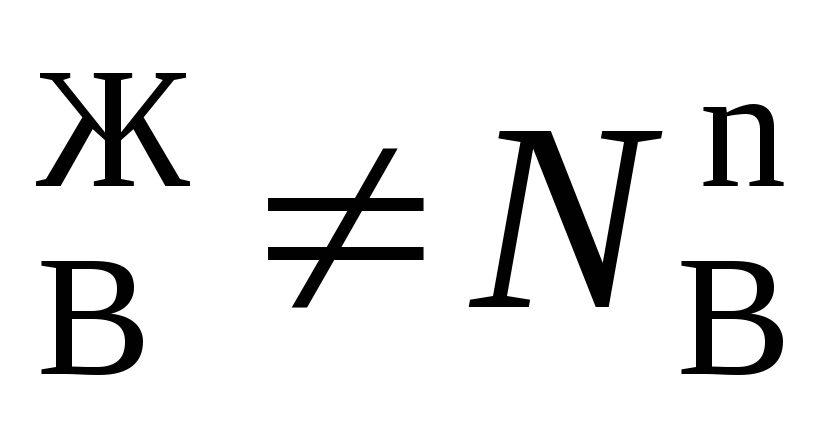. Эти неравенства отражают суть первого закона Коновалова. Для его уяснения обратимся к рисунку.

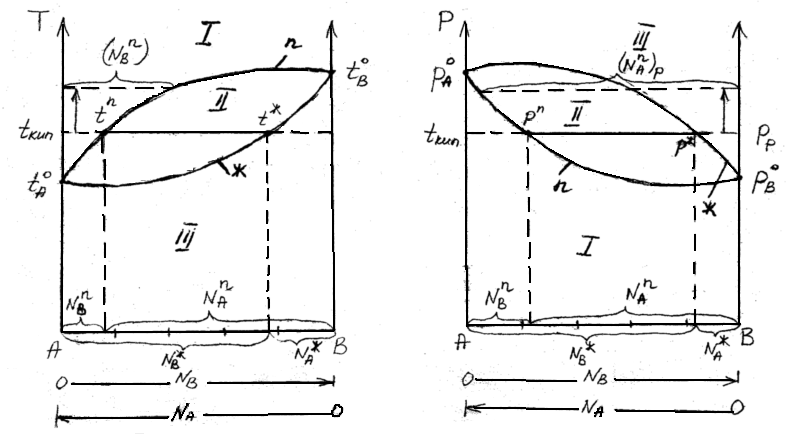
В соответствии с правилом фаз Гиббса в двух компонентной равновесной системе из четырех параметров (температура, давление, составы обеих фаз) только два являются независимыми (Т и р). При заданных значениях Т ирв равновесии находятся жидкость и пар фиксированного состава. Если же из двух независимых величин одна не изменяется (р=constили Т=const), то температура в первом случае и давление во втором однозначно определяются составом любой из существующих фаз.

Равновесие между раствором и паром удобно рассматривать в виде диаграмм, выражающих зависимость от состава системы температуры кипения жидкости (при р=const) или давления пара (при Т=const) . На диаграмме состояния по оси абсцисс справа на лево отложена мольная доля компонента, имеющего в чистом виде более низкую температуру кипения (на нашем первом рисунке компонент А более летуч,t) и более высокое давление насыщенного пара (на втором рисункер).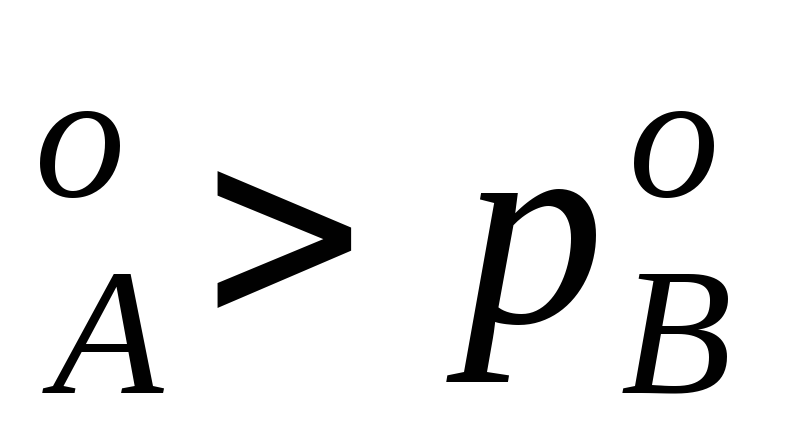

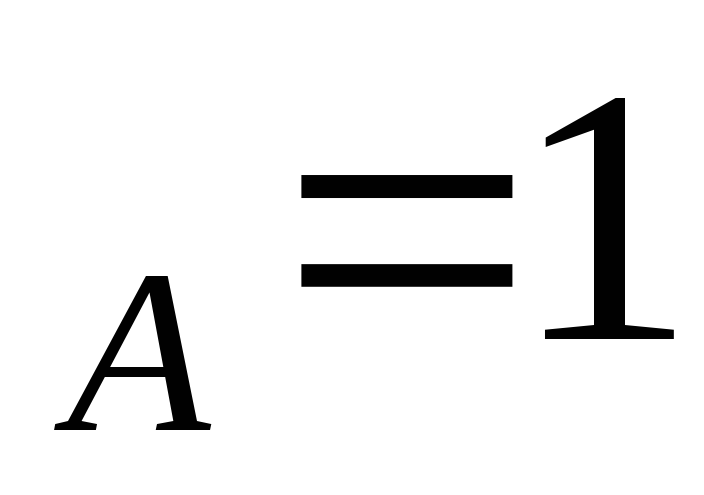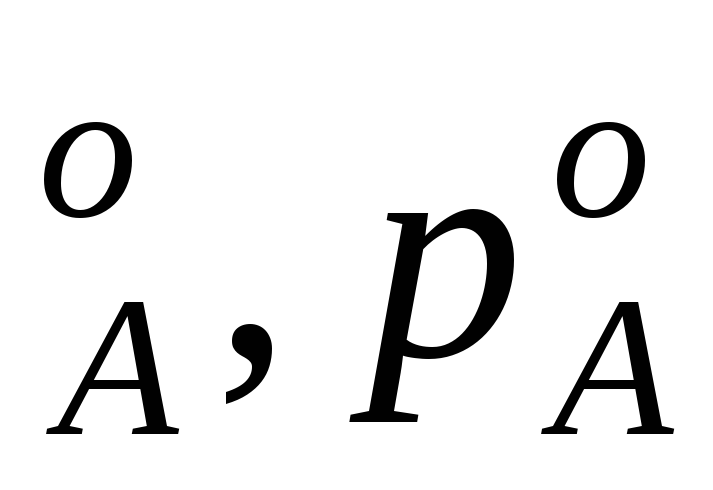Концевые точки оси абсцисс соответствуют чистым компонентам N,tиN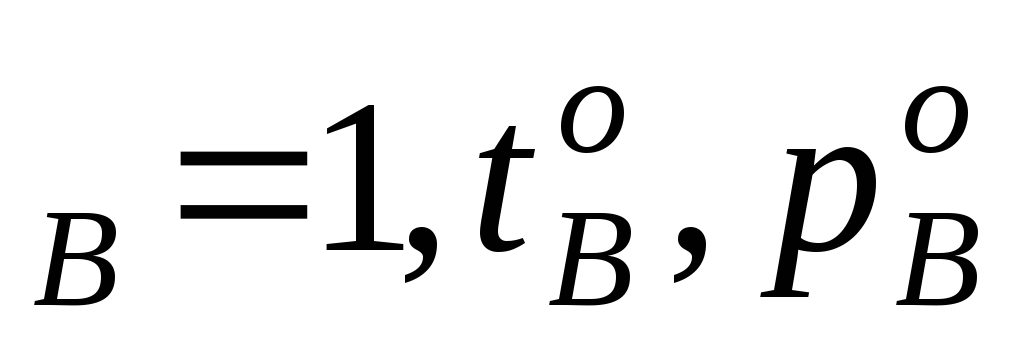. У раствора мольная доля компонентов А и В изменяется в диапазоне 0 Стр 1 из 3 1 2 3

studfiles.net