Правила построения эпюры

Правила построения эпюр поперечных сил и изгибающих моментов

Эпюры поперечных сил Q и изгибающих моментов М представляют собой графическое изображение этих величин по длине балки. Для построения этих эпюр определяют численное значение поперечных сил Q и изгибающих моментов М для ряда сечений балки и по ним строят соответствующие графики. Правило знаков для Q и М:

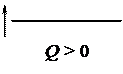
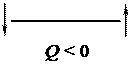
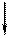
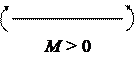
В качестве примера на рис. 16 приводятся эпюры Q и М для балок с различным видом нагружения.

Перечислим основные свойства эпюр Q и М, которые являются следствием дифференциальных зависимостей.

1. На участке, где нет распределенной нагрузки (q = 0), поперечная сила Q постоянна, а изгибающий момент изображается наклонной прямой линией (рис. 16 а, г).

2. На участках с постоянной равномерно распределенной нагрузкой (q = const) эпюра Q линейная, а эпюра М изображает квадратичную параболу (рис. 16 б, в). Кривизна параболы имеет знак распределенной нагрузки.

3. В точках приложения сосредоточенных сил эпюра Q имеет скачки, равные сосредоточенным силам, а эпюра М – изломы (рис. 16 а), острие которых направлено навстречу сосредоточенной силе.

4. В точках приложения сосредоточенных моментов эпюра М имеет скачки, равные сосредоточенным моментам; на эпюру Q сосредоточенные моменты не влияют (рис. 16 г).

5. В точках, где поперечная сила Q равна нулю, касательная к эпюре М горизонтальная, т.е. момент М имеет максимальное или минимальное значение.

mydocx.ru

Методика построения эпюр изгибающих моментов, поперечных и продольных сил

1. Виды опорных закреплений

С технической точки зрения опорные закрепления конструкций весьма разнообразны. При решении задач сопромата, все многообразие существующих опорных устройств схематизируется в виде ряда основных типов опор, из которых

наиболее часто встречаются: шарнирно-подвижнаяопора (возможные обозначения для нее представлены на рис.1,а), шарнирно-неподвижная опора (рис.1,б) и жесткое защемление, или заделка (рис.1,в).

В шарнирно-подвижной опоре возникает одна опорная реакция, перпендикулярная опорной плоскости. Такая опора лишает опорное сечение одной степени свободы, то есть препятствует смещению в направлении опорной плоскости, но допускает перемещение в перпендикулярном направлении и поворот опорного сечения.
В шарнирно-неподвижной опоре возникают вертикальная и горизонтальная реакции. Здесь невозможны перемещения по направлениям опорных стержней, но допускается поворот опорного сечения.
В жесткой заделке возникают вертикальная и горизонтальная реакции и опорный (реактивный) момент. При этом опорное сечение не может смещаться и поворачиваться.При расчете систем, содержащих жесткую заделку, возникающие опорные реакции можно не определять, выбирая при этом отсеченную часть так, чтобы заделка с неизвестными реакциями в нее не попадала. При расчете систем на шарнирных опорах реакции опор должны быть определены обязательно. Уравнения статики, используемые для этого, зависят от вида системы (балка, рама и др.) и будут приведены в соответствующих разделах настоящего пособия.

2. Построение эпюр продольных сил N z

Продольная сила в сечении численно равна алгебраической сумме проекций всех сил, приложенных по одну сторону от рассматриваемого сечения, на продольную ось стержня.

Правило знаков для Nz: условимся считать продольную силу в сечении положительной, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части стержня, вызывает растяжение и отрицательной — в противном случае.

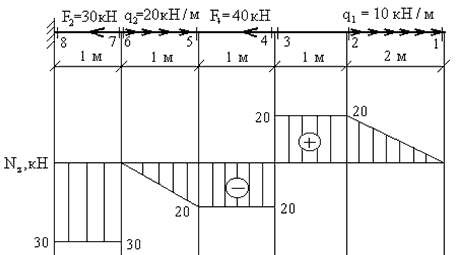
Пример 1.Построить эпюру продольных сил для жестко защемленной балки (рис.2).

1. Намечаем характерные сечения, нумеруя их от свободного конца стержня к заделке.
2. Определяем продольную силу Nz в каждом характерном сечении. При этом рассматриваем всегда ту отсеченную часть, в которую не попадает жесткая заделка.

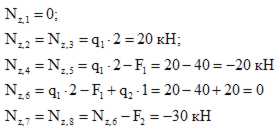
По найденным значениям строим эпюру Nz. Положительные значения откладываются (в выбранном масштабе) над осью эпюры, отрицательные — под осью.

3. Построение эпюр крутящих моментов М кр .

Крутящий момент в сечении численно равен алгебраической сумме внешних моментов, приложенных по одну сторону от рассматриваемого сечения, относительно продольной оси Z.

Правило знаков для Мкр: условимся считать крутящий момент в сечении положительным, если при взгляде на сечение со стороны рассматриваемой отсеченной части внешний момент виден направленным против движения часовой стрелки и отрицательным — в противном случае.

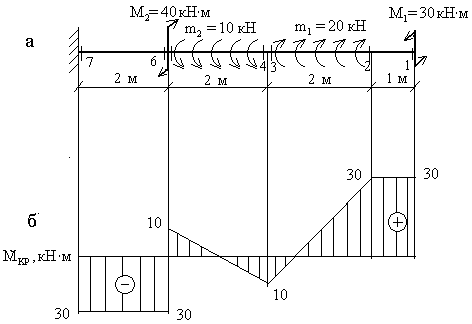
Пример 2.Построить эпюру крутящих моментов для жестко защемленного стержня (рис.3,а).

Следует отметить, что алгоритм и принципы построения эпюры крутящих моментов полностью совпадают с алгоритмом и принципами построения эпюры продольных сил.

1.Намечаем характерные сечения.
2.Определяем крутящий момент в каждом характерном сечении.

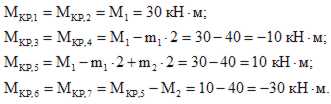
По найденным значениям строимэпюру Мкр (рис.3,б).

4. Правила контроля эпюр N z и М кр .

Для эпюр продольных сил и крутящих моментов характерны определенные закономерности, знание которых позволяет оценить правильность выполненных построений.

1. Эпюры Nz и Мкр всегда прямолинейные.

2. На участке, где нет распределенной нагрузки, эпюра Nz(Мкр) — прямая, параллельная оси, а на участке под распределенной нагрузкой — наклонная прямая.

3. Под точкой приложения сосредоточенной силы на эпюре Nz обязательно должен быть скачок на величину этой силы, аналогично под точкой приложения сосредоточенного момента на эпюре Мкр будет скачок на величину этого момента.

5. Построение эпюр поперечных сил Q y и изгибающих моментов M x в балках

Стержень, работающий на изгиб, называется балкой. В сечениях балок, загруженных вертикальными нагрузками, возникают, как правило, два внутренних силовых фактора — поперечная сила Qy и изгибающий момент Mx .

Поперечная сила в сечении численно равна алгебраической сумме проекций внешних сил, приложенных по одну сторону от рассматриваемого сечения, на поперечную (вертикальную) ось.

Правило знаков для Qy: условимся считать поперечную силу в сечении положительной, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, стремится повернуть данное сечение по часовой стрелке и отрицательной — в противном случае.

Схематически это правило знаков можно представить в виде

Изгибающий момент Mx в сечении численно равен алгебраической сумме моментов внешних сил, приложенных по одну сторону от рассматриваемого сечения, относительно оси x , проходящей через данное сечение.

Правило знаков для Mx: условимся считать изгибающий момент в сечении положительным, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, приводит к растяжению в данном сечении нижних волокон балки и отрицательной — в противном случае.

Схематически это правило знаков можно представить в виде:

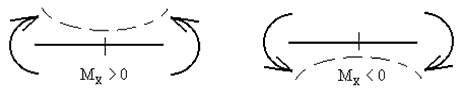
Следует отметить, что при использовании правила знаков для Mx в указанном виде, эпюра Mx всегда оказывается построенной со стороны сжатых волокон балки.

6. Консольные балки

При построении эпюр Qy и Mx в консольных, или жестко защемленных, балках нет необходимости (как и в рассмотренных ранее примерах) вычислять опорные реакции, возникающие в жесткой заделке, но выбирать отсеченную часть нужно так, чтобы заделка в нее не попадала.

Пример 3.Построить эпюры Qy и Mx (рис.4).

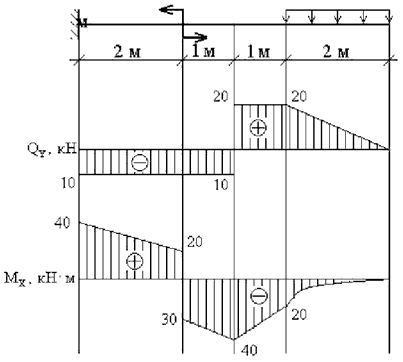
1. Намечаем характерные сечения.

2. Определяем поперечную силу Qy в каждом характерном сечении.

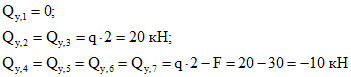
По вычисленным значениям строим эпюру Qy.

3. Определяем изгибающий момент Mx в каждом характерном сечении.

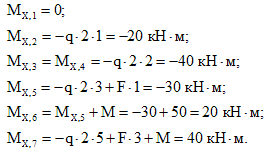
По вычисленным значениям строим эпюру Mx, причем, на участке под распределенной нагрузкой эпюра будет криволинейной (квадратная парабола). Выпуклость кривой на этом участке всегда обращена навстречу распределенной нагрузке.

7. Балки на двух опорах

В отличие от консольных балок, при расчете балок на двух шарнирных опорах необходимо сначала определить опорные реакции из уравнений статики, так как и в левую, и в правую отсеченные части для любого сечения, расположенного между опорами, попадает соответствующая реакция.

Для плоской системы число уравнений статики в общем случае равно трем. Если балка загружена только вертикальными нагрузками, то горизонтальная реакция шарнирно-неподвижной опоры равна нулю, и одно из уравнений равновесия обращается в тождество. Таким образом, для определения реакций в опорах шарнирной балки используются два уравнения статики:

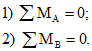
Пример 4. Построить эпюры Qy, Mx для балки с шарнирным опиранием (рис.5).

1. Вычисляем реакции опор.

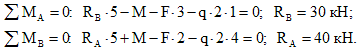
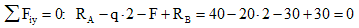
2. Намечаем характерные сечения.

В отличие от консольных балок здесь известны обе опорные реакции, поэтому для любого сечения можно рассматривать как левую, так и правую отсеченную часть.

3. Определяем поперечные силы в характерных сечениях.

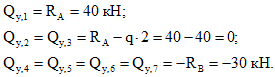
Строим эпюру Qy.

4. Определяем изгибающие моменты в характерных сечениях.

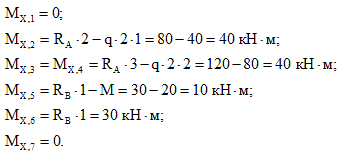
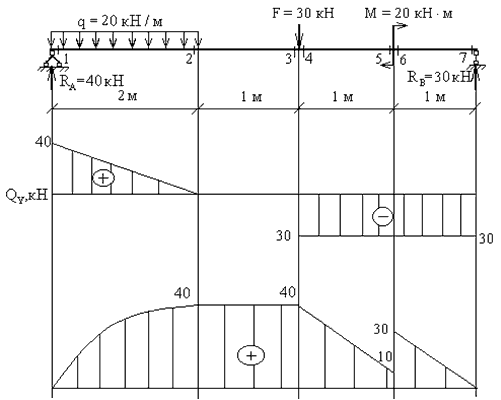
Строим эпюру Mx.

8. Правила контроля эпюр Q у и M x

Дифференциальные зависимости между q, Qy, Mx определяют ряд закономерностей, которым подчиняются эпюры Qy и Mx.

Эпюра Qy является прямолинейной на всех участках; эпюра Mx — криволинейная (квадратная парабола) на участке под равномерно распределенной нагрузкой, причем, выпуклость кривой всегда обращена навстречу нагрузке q, и прямолинейная на всех остальных участках.

Под точкой приложения сосредоточенной силы (реакции) на эпюре Qy обязательно должен быть скачок на величину этой силы (реакции). Аналогично, под точкой приложения сосредоточенного момента на эпюре Mx обязателен скачок на величину момента.

Если на участке под распределенной нагрузкой эпюра Qy пересекает ось (Qy=0), то эпюра Mx в этом сечении имеет экстремум.

На участках с поперечной силой одного знака эпюра Mx имеет одинаковую монотонность. Так, при Qy>0 эпюра Mx возрастает слева направо; при Qy

funnystudy.ru

шпоргалка / подготовка к ЭКЗАМЕНУ / 52.Основные правила построения эпюр поперечных сил и изгибающих моментов

52.Основные правила построения эпюр поперечных сил и изгибающих моментов.

1.7 ПОСТРОЕНИЕ ЭПЮР ПОПЕРЕЧНЫХ СИЛ И ИЗГИБАЮЩИХ МОМЕНТОВ В БАЛКАХ Стержень, работающий на изгиб, называется балкой. В сечениях балок, загруженных вертикальными нагрузками, возникают, как правило, два внутренних силовых фактора — поперечная сила и изгибающий момент . Поперечная сила в сечении численно равна алгебраической сумме проекций внешних сил, приложенных по одну сторону от рассматриваемого сечения, на поперечную (вертикальную) ось. Правило знаков для : условимся считать поперечную силу в сечении положительной, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, стремится повернуть данное сечение по часовой стрелке и отрицательной — в противном случае. Схематически это правило знаков можно представить в виде Изгибающий момент в сечении численно равен алгебраической сумме моментов внешних сил, приложенных по одну сторону от рассматриваемого сечения, относительно оси x , проходящей через данное сечение. Правило знаков для : условимся считать изгибающий момент в сечении положительным, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, приводит к растяжению в данном сечении нижних волокон балки и отрицательной — в противном случае. Схематически это правило знаков можно представить в виде: Следует отметить, что при использовании правила знаков для в указанном виде, эпюра всегда оказывается построенной со стороны сжатых волокон балки. 1.8 КОНСОЛЬНЫЕ БАЛКИ При построении эпюр и в консольных, или жестко защемленных, балках нет необходимости (как и в рассмотренных ранее примерах) вычислять опорные реакции, возникающие в жесткой заделке, но выбирать отсеченную часть нужно так, чтобы заделка в нее не попадала.

studfiles.net

Техническая механика

Сопротивление материалов

Построение эпюр в сопромате

Прикладное значение науки сопротивление материалов заключается в возможности определения основных критериев работоспособности деталей машин и различных конструкций – прочности, деформации и устойчивости.
Применяя метод сечений в сочетании с приемами статики и других разделов прикладной механики, можно определить напряжения, возникающие в том или ином сечении бруса (детали, элемента конструкции), и, исходя из анализа полученного результата, сделать выводы о работоспособности этого бруса при приложении к нему расчетных нагрузок.
Именно напряжение является основным фактором, влияющим на прочностные характеристики элемента конструкции, а также его способность противостоять деформации. По этой причине в сопромате главной задачей, чаще всего, является определение напряжений, возникающих в том или ином сечении детали или элемента конструкции.

Для удобства анализа напряженности отдельных участков и сечений конструкции (бруса) используют графическое изображение нагрузок и напряжений в каждом сечении. Это позволяет визуально анализировать распределение нагрузок и напряжений по всей длине бруса, определять при этом наиболее нагруженные (критические) участки и сечения. Такие графические изображения нагрузок, напряжений, а также деформаций элементов конструкций называют эпюрами.

При анализе степени напряженности и деформирования элемента конструкции (детали, бруса) наиболее часто производят построение следующих типов эпюр:

• эпюры внутренних сил (продольных или поперечных), действующих в сечениях бруса;
• эпюры вращающих (крутящих) моментов;
• эпюры изгибающих моментов;
• эпюры напряжений (нормальных или касательных);
• эпюры перемещений (удлинений, укорочений, прогибов и т. п.).

Иногда на одной эпюре показываются несколько внутренних силовых факторов (эпюра продольных и поперечных сил, эпюра изгибающего и вращающего моментов), но такие эпюры при сложных нагрузках и переменных сечениях бруса сложны для чтения.

Как упоминалось выше, наиболее важную информацию о прочностных характеристиках элемента конструкции (бруса), т. е. способности противостоять разрушению, можно получить, используя эпюры напряжений, а информацию о степени деформации под действием расчетной нагрузки – по эпюрам перемещений.
Эпюры внутренних усилий и моментов в большинстве случаев не дают полной информации о степени напряженности и деформирования отдельных сечений и участков бруса, а являются промежуточным звеном при построении эпюр напряжений и перемещений, особенно если брус имеет ступенчатую форму или переменное поперечное сечение по длине.



Правила построения эпюр

При построении эпюр придерживаются определенных стандартных правил, позволяющих одинаково читать, истолковывать и анализировать эпюру всем участникам процесса конструирования изделия.

Построение эпюры начинают с изображения нулевой линии, которая символизирует линию бруса в ненапряженном состоянии. При этом, если брус имеет сложную пространственную форму, нулевая линия эпюры повторяет контуры центральной (осевой) линии бруса, и имеет такую же пространственную форму.

Нулевую линию эпюры обозначают названием и нулевым символом. Слева от нулевой линии указывается название эпюры (эпюра сил, моментов, напряжений и т. п.), справа от нулевой линии ставится цифра « 0 ». При указании называния эпюры обычно используют символ изображаемой нагрузки, например, внутренние продольные силы чаще всего обозначаются буквой « N », поперечные – буквой « Q », эпюры изгибающих моментов – буквами « M_из », эпюры вращающих моментов – буквами « Т » или « M_кр », эпюры напряжений – буквами « σ » или « τ » и т. п. Рядом с буквенным названием эпюры (или под ним) указывается единица измерения (ньютон, мегапаскаль, мм и т. п.).

Следующий этап построения эпюры – определение границ силовых участков бруса, т. е. таких участков, где внутренний силовой фактор в сечениях или деформация бруса изменяются по одной закономерности (или остаются постоянными). Как правило, границами силовых участков являются сечения, где приложена внешняя нагрузка или (и) площадь поперечного сечения бруса изменяется. В некоторых случаях, при построении эпюр брусьев сложной объемной формы, границы участков определяют аналитически. Границы силовых участков обозначаются тонкими вертикальными линиями, проведенными от изображения бруса через все эпюры.

Для оптимальной наглядности графика эпюры важно правильно выбрать масштаб изображаемого силового фактора, напряжения или деформации. Если масштаб окажется слишком мелким – эпюра будет трудна для чтения и анализа, если слишком крупным – она займет много места на чертеже.
Если учесть, что для одного бруса выполняют, как правило, несколько эпюр, расположенных одна под другой, то крупный масштаб не позволит выполнить построение эпюр на одном листе.
Для правильного выбора масштаба эпюры предварительно следует просчитать значение отображаемого фактора по всем контрольным сечениям бруса, и после этого определиться с масштабом.
Если, например, в результате расчетов окажется, что вся эпюра займет положительную область (над нулевой линией), то при построении графика эпюры это следует учесть.

Положительные значения фактора откладываются вверх от нулевой линии, отрицательные – вниз. Если на каком-либо участке силовой фактор равен нулю, эпюра совпадает с нулевой линией по всей длине этого участка. После построение внешнего контура эпюры на контрольных сечениях проставляются значения фактора (обычно на внешних углах эпюры), при этом знак фактора (плюс или минус) не указываются.
На положительной области (в самой широкой части) ставится знак «+» в кружке, а на отрицательной области – знак «—» в кружке (см. примеры построения эпюр). Иногда знаки «+» и «—» на эпюре указываются сверху и снизу цифры « 0 » (справа нулевой линии), тогда на площади графика эпюры эти знаки (в кружках) не ставятся.

По окончании построения эпюры по ее площади проводят тонкие вертикальные линии через равные промежутки. Эти линии символизируют сечения бруса. Иногда, в случае построения сложной пространственной эпюры, линии выполняют не вертикально, а в соответствии с проекционным направлением участка на графике эпюры.



Определение знака фактора на эпюре

При построении эпюр внутренних силовых факторов или деформаций необходимо правильно определять знак фактора на данном силовом участке бруса. Для этого следует пользоваться следующими общепринятыми правилами:

• сжимающая продольная нагрузка считается отрицательной, растягивающая – положительной;
• поперечная сила Q , направленная вниз считается отрицательной, вверх – положительной;
• вращающий (крутящий) момент считается положительным, если он вращает «отсеченную» часть бруса против часовой стрелки, отрицательным – по часовой;
• эпюра изгибающих моментов строится в соответствии с «правилом дождя». Это правило используется следующим образом: если в результате деформации от изгибающего момента исследуемое сечение прогнулось вниз, значит, эпюра имеет положительное значение (образовалась «воронка», в которой может задерживаться «дождевая вода»); если же балка прогнулась вверх, то эпюра имеет отрицательное значение («вода» будет скатываться с балки). Более подробно о знаках эпюр поперечных сил и изгибающих моментов здесь.

Особенности построения эпюр поперечных сил и изгибающих моментов

Для облегчения построения эпюр и контроля правильности графика следует запомнить ряд правил, вытекающих из теоремы Журавского:

На участке, где равномерно распределенная нагрузка q отсутствует, эпюра поперечных сил Q представляет собой прямую линию, параллельную нулевой линии (оси бруса), а эпюра изгибающих моментов M_из – наклонную прямую.

В сечении, где приложена сосредоточенная сила, на эпюре Q должен быть ступенчатый скачок на величину этой силы, а на эпюре M_из – излом (изменение направления графика).

На участке действия равномерно распределенной нагрузки q эпюра Q представляет собой наклонную прямую, а эпюра M_из – параболу, обращенную выпуклостью навстречу стрелкам, изображающим направление распределенной нагрузки.

Если эпюра Q на наклонном участке в каком-либо сечении пересекает нулевую линию эпюры, то в этом сечении на эпюре изгибающих моментов M_из будет иметь экстремальное значение (минимальное или максимальное).

Если на границе действия распределенной нагрузки нет сосредоточенных сил, то наклонный участок эпюры Q соединяется с горизонтальным без «ступеньки», а параболический участок эпюры M_из соединяется с наклонным участком плавно, без излома.

В сечениях, где к брусу приложены сосредоченные пары сил, на эпюре M_из будут иметь место ступенчатые скачки на величину действующих внешних моментов, а эпюра Q изменения не претерпевает (приложенные к брусу изгибающие моменты не влияют на эпюру поперечных сил).

Примеры построения эпюр

Материалы раздела «Сопротивление материалов»:

k-a-t.ru

Правила построения и контроля правильности построения эпюр внутренних силовых факторов

Из рассмотренных примеров, как следствия дифференциальных зависимостей между , и , вытекают следующие правила.

1. В сечениях, где приложены сосредоточенные силы, на эпюрах продольной и поперечной сил происходит скачек на величину этих сил в направлении их действия, а эпюра изгибающего момента претерпевает излом в сторону действия сосредоточенных сил.

2. На участках стержней, где отсутствует равномерно распределенная нагрузка, продольная и поперечная сила величины постоянные, а эпюра изгибающего момента изменяется по закону наклонной прямой.

3. На участках, где приложена равномерно распределенная нагрузка, эпюры продольной и поперечной сил изменяются по закону наклонной прямой на величину равнодействующей распределенной нагрузки. При положительном значении распределенной нагрузки эпюры возрастают, при отрицательном – убывают.

4. В сечениях на свободном или шарнирно опертом концах балки, где отсутствует сосредоточенный изгибающий момент, изгибающий момент равен нулю.

5. На участках, где приложена поперечная равномерно распределенная нагрузка, эпюра изгибающего момента изменяется по закону квадратной параболы, выпуклостью навстречу направлению действия распределенной нагрузки.

6. В сечениях, где приложен сосредоточенный изгибающий момент, на эпюре изгибающего момента происходит скачек на его величину в направлении его действия.

7. В сечении, где поперечная сила равна нулю, изгибающий момент имеет экстремальное значение.

8. На участках, где поперечная сила равна нулю, изгибающий момент величина постоянная.

9. На участках, где поперечная сила положительна, эпюра изгибающего момента возрастает, где отрицательна – убывает.

10. Изгибающий момент в любом сечении равен площади эпюры поперечной силы левой или правой отсеченной части балки плюс приложенные к ним сосредоточенные изгибающие моменты.

Вопросы и ответы для самоконтроля

1. Что называется главным вектором внутренних сил ?

Равнодействующий вектор внутренних сил, приложенный в центре тяжести сечения, называется главным вектором внутренних сил.

2. Что называется главным моментом внутренних сил ?

Равнодействующий момент внутренних сил, действующий относительно центра тяжести сечения, называется главным моментом внутренних сил.

3. Что называется внутренними силовыми факторами ?

Проекции главного вектора и главного момента внутренних сил на оси подвижной системы координат, помещенной началом в центре тяжести сечения, называются внутренними силовыми факторами.

4. Гипотеза плоских сечений.

Сечения плоские и перпендикулярные оси стержня до деформации при простых состояниях стержня, остаются плоскими и перпендикулярными оси стержня после деформации.

5. Чему равна продольная сила в любом сечении ?

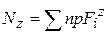— продольная сила в любом сечении равна алгебраической сумме проекций всех внешних сил, действующих на отсеченную часть стержня, на продольную ось z.

6. Чему равны поперечные силы в любом сечении ?

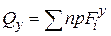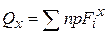, — поперечные силы в любом сечении равны алгебраической сумме проекций всех внешних сил, действующих на отсеченную часть стержня, на поперечные оси y, x.

7. Чему равен крутящий момент в любом сечении ?

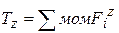— крутящий момент в любом сечении равен алгебраической сумме моментов всех внешних сил, действующих на отсеченную часть стержня, относительно оси z.

8. Чему равны изгибающие моменты в любом сечении ?

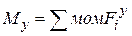, — изгибающие моменты в любом сечении равны алгебраической сумме моментов всех внешних сил, действующих на отсеченную часть стержня, относительно осей х, y.

9. Что показывают эпюры внутренних силовых факторов ?

Эпюры внутренних силовых факторов показывают графический закон их изменения вдоль продольной оси стержня.

10. Для чего строятся эпюры внутренних силовых факторов ?

Эпюры внутренних силовых факторов строятся для определения закона их изменения по длине стержня и определения сечений с их максимальным значением.

11. Какое состояние называется растяжением-сжатием ?

Состояние стержня, при котором в его сечениях действует продольная сила, называется растяжением-сжатием.

12. Какое состояние называется чистым сдвигом ?

Состояние стержня, при котором в его сечениях действует поперечная сила, называется чистым сдвигом.

13. Какое состояние называется кручением ?

Состояние стержня, при котором в его сечениях действует крутящий момент, называется кручением.

14. Какое состояние называется чистым изгибом ?

Состояние стержня, при котором в его сечениях действует только изгибающий момент, называется чистым изгибом.

15. Какое состояние называется поперечным изгибом ?

Состояние стержня, при котором в его сечениях действует одновременно поперечная сила и изгибающий момент, называется поперечным изгибом.

16. Системы подвижных координат для отсеченных частей стержня. Рисунок 3.12

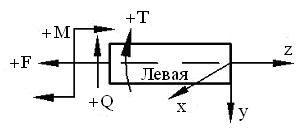
17. Правила знаков при определении внутренних силовых факторов. Рисунок 3.12

Проекции внешних продольных сил положительны, если они направлены от рассматриваемого сечения.

Проекции внешних поперечных сил положительны, если они направлены вверх слева от сечения и вниз справа от сечения.

Крутящий момент от внешних нагрузок положителен, если он действует по часовой стрелке относительно оси z любой отсеченной части стержня.

Изгибающий момент от внешних нагрузок положителен, если он действует по часовой стрелке относительно поперечной оси слева от сечения и против часовой стрелке справа от сечения.

18.Дифференциальные зависимости между интенсивностью внешних распределенных нагрузок и внутренними силовыми факторами.

, , ,

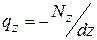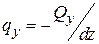19. Дифференциальные зависимости между внутренними силовыми факторами.

, .

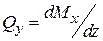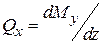Дата добавления: 2014-12-06 ; просмотров: 1646 . Нарушение авторских прав

studopedia.info