Сдвиг Закон гука для сдвига

Напряженное состояние, изображенное на рис. 4.4, а, представляет собой чистый сдвиг. В этом состоянии длины ребер элементарного параллелепипеда не изменяются, а изменяются лишь углы между боковыми гранями: первоначально прямые углы становятся равными 90° (рис. 4.4, б).

Каждая из граней параллелепипеда при деформации чистого сдвига перемещается относительно противоположной грани на величину АА, называемую абсолютным сдвигом (рис. 4.4, б). Отношение абсолютного сдвига к расстоянию между противоположными гранями называется относительным сдвигом; при малых деформациях оно равно величине угла сдвига — изменения первоначально прямых углов между боковыми гранями параллелепипеда.

Абсолютный сдвиг выражается в мерах длины, а относительный сдвиг — в радианах. Величина у, как показывает опыт, прямо пропорциональна величине касательных напряжений. Эта зависимость между , называемая законом Гука при сдвиге, выражается в виде

Она справедлива при напряжениях, не превышающих предела пропорциональности материала.

Коэффициент пропорциональности G в формулах (3.4) и (4.4) называется модулем сдвига, или модулем упругости второго рода.

Модуль сдвига является физической постоянной материала, характеризующей его жесткость (т. е. способность сопротивляться упругим деформациям) при сдвиге. Модуль сдвига G, как и модуль упругости Е, выражается в кгс/см2, кгс/ммг, тс/м2 и т. д.

Деформации сдвига можно определять по формуле (3.4) не только при чистом сдвиге, но и в общем случае плоского напряженного состояния — когда по боковым граням параллелепипеда действуют не только касательные, но также и нормальные напряжения. Это является следствием того, что нормальные напряжения вызывают лишь поступательные перемещения боковых граней параллелепипеда и не вызывают изменения его прямых углов.

stu.sernam.ru

Сдвиг Закон гука для сдвига

,

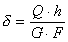где G — модуль сдвига или модуль упругости второго рода. Можно показать, что модуль сдвига связан с модулем упругости первого рода и коэффициентом Пуассона следующим, хорошо согласующимся с опытом, уравнением:

.

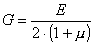Для стали модуль сдвига G=8·10 4 МПа.

Из уравнения (5.2) с учетом (5.1) может быть получен закон Гука при сдвиге в относительных координатах:

.

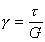
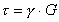Закон Гука справедлив лишь до предела пропорциональности. При испытаниях на сдвиг образцов из пластичных материалов так же, как и при растяжении, наблюдается явление текучести. Предел текучести обозначается через τ_т, а предел прочности – через τ_в.

Связь между тремя постоянными упругого материала.

a) Модуль упругости первого рода: – устанавливает прямую пропорциональность между напряжениями и деформациями. Измеряется в паскалях.

b) Коэффициент Пуассона: — Характеризует свойства материала. Устанавливает прямую пропорциональность между поперечной и продольной деформациями.

c) Модуль сдвига или модуль упругости второго рода: 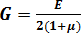–закон Гука для сдвига. Измеряется в тех же единицах, что и E. Отражает связь между упругими постоянными.

29. Деформация чистого кручения. Напряжение при кручении. Рациональная форма сечения.

Кручением называют такой вид деформации, когда в поперечных сечениях возникает единственный силовой фактор – крутящий момент.

Напряжение и деформации при кручении

При кручении возникает напряжённое состояние, называемое «чистый сдвиг» (рис. 456).

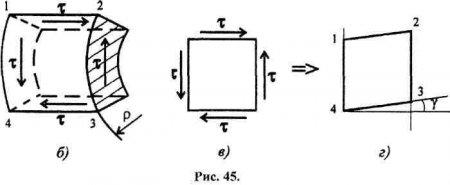
При сдвиге на боковой поверхности элемента 1234 возникают касательные напряжения, равные по величине (рис. 45в), элемент деформируется (рис. 45г). Материал подчиняется закону Гука. Касательное напряжение пропорционально углу сдвига.

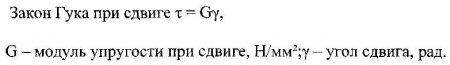
Рациональные формы сечений при кручении.

Из двух сечений с одним и тем же полярным моментом сопротивления (или в случае некруглого сечения одним и тем же Wк), а следовательно, с одним и тем же допускаемым крутящим моментом, рациональным будет сечение с наименьшей площадью, т.е. обеспечивающее наименьший расход материала. Так как отношение Wp/A (или Wк/A) является величиной размерной, то для сравнения различных сечений удобно применять безразмерную величину 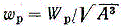(при некруглом сечении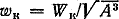), которую можно называть удельным моментом сопротивления при кручении. Чем больше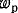, тем рациональнее сечение.

30. Внецентрическое сжатие коротких стержней. Внутренние усилия. Внецентренное сжатие – это вид деформации, при котором продольная сила в поперечном сечении стержня приложена не в центре тяжести. При внецентренном сжатии, помимо продольной силы (N), возникают два изгибающих момента (M_x и M_y).

Рассмотрим, какие внутренние силы при внецентренном сжатии действуют на стержень в поперечном сечении. Пусть сжимающая сила (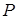) приложена в некоторой точке A с координатамиивглавных центральных осяхинерции x и y (см. рис. 10.1, а).

С учетом допущения, что стержень обладает большой жёсткостью на изгиб: .

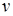Формула изгибающих моментов при внецентренном сжатии с учетом прогибов: , гдеи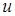прогибы рассматриваемого поперечного сечения стержня в направлении осе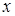йи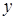, соответственно. Наше допущение о большой жесткости стержня на изгиб заключается в предположении:.

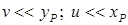Нормальные напряжения в произвольной точке 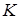(см. рис. 10.1) с координатамии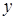будут равны: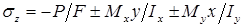, где, согласно принципу независимости действия сил, первое слагаемое — напряжение от сжатия, а второе и третье – от изгиба.

Значения изгибающих моментов и координат исследуемой точки 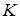подставляются в формулупо абсолютному значению, а знак второго и третьего слагаемых определяется по физическому смыслу.

studfiles.net

Сдвиг (срез). Закон Гука при сдвиге. Смятие

С этим видом деформации каждый из Вас многократно сталкивался, когда что-либо резал ножницами. Особенно характерно проявляется последовательность деформации (сначала сдвиг, а затем срез) если ножницы тупые и разболтанные. Обратите внимание на срез листового металла после гильотинных ножниц. Срез не перпендикулярен плоскости листа, а слегка наклонен, кроме того по направлению реза тянется заусенец. Представим эту деформацию графически

Силы F – это силы, создающиеся лезвиями ножниц. Вся деформация происходит в зоне прямоугольника abcd, который в результате деформации превращается в паралелограм.

Величина cc1 ≈ dd1 называется абсолютным сдвигом.

cc1/bc = tg γ ≈ γ – относительный сдвиг.

При сдвиге в сечении возникает только поперечная сила Q, следовательно и только касательные напряжения τ. Условие прочности записывается так:

τ = Q/А ≤ [τ] условие прочности при сдвиге (срезе)

При сдвиге (как и при растяжении) существует зависимость между напряжением и деформацией. Эта зависимость выражается законом Гука.

τ = G*γ — напряжения пропорциональны относительному сдвигу (Закон Гука).

G – модуль сдвига (МПа). Между модулем упругости Е и модулем сдвига G существует зависимость

G = Е/[2(1 + μ)], где μ – коэффициент Пуассона

При работе конструкций (особенно в динамическом режиме) в элементах соединений (болтовых, шпоночных и др.) возникает деформация смятия. Сечение элемента искажается, например, круглое сечение становится овальным, боковая поверхность шпонки увеличивается в размерах, при этом уменьшается ширина шпонки и т.д. В результате в соединении появляются не допустимые зазоры и люфты. Поэтому заклепки, болты, шпонки и др. кроме расчета на сдвиг, проверяют на смятие.

Расчетная схема заклепки на смятие показана на рис.1.11.

Боковая поверхность заклепки сминается (сжимается), следовательно на поверхности возникают нормальные напряжения σсм. Условие прочности запишем в виде

σсм = F/Асм ≤ [σ]см — условие прочности на смятие

Очевидно, что смять (раздавить) стержень труднее, чем его разорвать. Следовательно [σ]см > [σ]. Рекомендуется [σ]см ≈ 2[σ].

studopedia.ru

Энциклопедия по машиностроению XXL

Оборудование, материаловедение, механика и .

Гука закон при сдвиге

Закон Гука при чистом сдвиге. Зависимость между нагрузкой и деформацией при сдвиге можно проследить по так называемой диаграмме сдвига (рис. 185). Для пластичных материалов она аналогична диаграмме растяжения. На диаграмме показаны характеристики прочности — Тпц, Тт и т . [c.198]

При сдвиге также справедлив закон Гука [c.143]

Касательное напряжение определяем, пользуясь законом Гука при сдвиге х = Gy = 80 -10 1 10″ = 80 МПа. [c.141]

Закон Гука при сдвиге справедлив, пока напряжения т не превысят предела пропорциональности при сдвиге т ц. [c.228]

Напряжения и деформации при сдвиге связаны между собой зависимостью, которая называется законом Гука при сдвиге. [c.210]

Закон Гука при сдвиге справедлив лишь в определенных пределах нагружения и формулируется так касательное напряжение прямо пропорционально относительному сдвигу. [c.210]

Таким образом, мы видим, что упругие свойства изотропной среды определяются не тремя, а всего двумя независимыми константами. И если при растяжении закон Гука нами постулировался, то при сдвиге его можно рассматривать как следствие уже принятой пропорциональности между нормальным напряжением и удлинением. [c.47]

По аналогии с законом Гука для линейной деформации дается закон Гука, аля угловой деформации (при сдвиге). Разъясняется физический смысл модуля сдвига О как физической постоянной материала, характеризующей его жесткость при сдвиге. В учебной литературе и в практике преподавания для величины О применяют различные наименования модуль сдвига, модуль упругости при сдвиге, модуль упругости второго рода. Не отрицая возможности применения любого из этих терминов, будем пользоваться первым из них как рекомендованным Комитетом технической терминологии АН СССР. [c.103]

Закон Гука при сдвиге можно изложить как следствие закона Гука при линейной деформации, этот путь показан в учебнике [36], но такая система изложения (тем более в техникумах) менее целесообразна, чем предложенная выше. [c.103]

Учитывая, что при сдвиге закон Гука записывается как г = Оу, в нашем случае имеем [c.121]

Имея в виду формулы (55) и (56). закон Гука при сдвиге можно записать следующим образом [c.58]

Связь между угловыми деформациями и касательными напряжениями, согласно закону Гука при сдвиге (г), можно представить независимо для каждой из трех плоскостей, параллельных координатным плоскостям [c.34]

По основанию С2 параллелепипеда в направлении сдвига, т. е. перпендикулярно радиусу р, действуют касательные напряжения т (рис. 6.7, б). Величина их на основании закона Гука при сдвиге равна [c.172]

Решение. Изменение (в данном случае — увеличение) прямого угла при сдвиге найдем из закона Гука [c.109]

Согласно закону Гука при сдвиге у = т/С и из (11.6) получаем, что [c.182]

Закон Гука при сдвиге. Пусть на брус (рис. 2.13, а) с площадью поперечного сечения Р действуют сдвигающие силы Р. Воспользуемся методом сечений. Мысленно отбросим часть бруса, лежащую справа от сечения т—т (рис. 2.13, б). Действие отброшенной части на оставшуюся заменим силами упругости интенсивности действующими в сечении т—т (рис. 2.13, в). Условие равновесия оставшейся части имеет вид [c.139]

Закон Гука при сдвиге, принимая во внимание выражения (2.16) и (2.18), можно записать в ином виде [c.139]

Напряжения. В соответствии с законом Гука при сдвиге можно записать [c.141]

На основании закона Гука при сдвиге имеем X = (jy == GpdtS /dz. [c.113]

Рассмотрим теперь вопрос о1.деФормациях при чистом сдвиве. Представим себе, что одна из граней элемента, выделенного площадками чистого сдвига, жестко закреплена (рис. 2.70). Тогда элемент примет вид, показанный на рисунке штриховыми линиями, т. е. деформация проявляется в изменении величин первоначально прямых углов между гранями элемента. Это изменение угла принято обозначать буквой и называть углом сдвига. Величина угла сдвига связана с величиной касательного напряжения законом Гукя при сдвиге [c.228]

Как уже указывалось выше, закон Гука справедлив для всех упругих тел, но только пока деформации не превосходят предела пропорциональности. Обычно при рассмотрении задач механики упругих тел предполагают, что деформации не превосходят этого предела. Это упр01цает все расчеты и позволяет применять принцип суперпозиции, который заключается в следующем. Представим себе, что мы подвергли тело какой-либо деформации, например растяжению, а затем другой деформации, например сдвигу. Пока предел пропорциональности не достигнут, модули и G, характеризующие упругие свойства тела, являются константами, не зависящими от того, деформировано уже тело или нет. Поэтому при сдвиге в теле возникнут такие же дополнительные напряжения т = G как и в том случае, если бы тело не было предварительно растянуто. Общее напряжение в теле будет представлять собой сумму тех напряжений, которые возникли бы, если бы тело было подвергнуто только растяжению или только сдвигу. Это и есть принцип суперпозиции (наложения) в применении к нашему конкретному случаю. Он справедлив потому, что упругие свойства тела не зависят от деформации (почему и соблюдается закон Гука). Пока всякая новая деформация вызывает такие же добавочные напряжения, как в отсутствие прежних деформаций, в результате многих деформаций получается напряжение, равное сумме всех тех напряжений, которые возникли бы, если бы каждая из деформаций существовала отдельно. [c.471]

Мы уже знаем, что между напряжениями и деформациями существуют различного рода зЛзисимости, характер которых устанавливается экспериментально. До сих пор эти зависимости рассматривались нами в частных проявлениях. Мы уже не раз писали условие пропорциональности между удлинением и нормальным напряжением и называли это условие законом Гука при растяжении. Мы не раз обращались к условию пропорциональности между касательными напряжениями и углами сдвига и называли это соотношение законом Гука при сдвиге. И вообще любые формы пропорциональности между силами и перемещениями, между напряжениями и деформациями мы для краткости связываем с именем Гука. Это просто и понятно. [c.39]

Не исключено, что некоторым преподавателям покажутся странными или сомнительными утверждения об отсутствии в этой теме, так сказать, чистой теории. Они возможно спросят А как же закон Гука.при сдриге Деформация сдвига Закон парности касательных напряжений Все эти вопросы не имеют отношения к данной теме, они рассматриваются при изучении чистого сдвига в, теме Кручение . Это вполне естественно, так как экспериментально чистый сдвиг можно осуществить только при кручении тонкостенной трубы. Мы останавливаемся на этом вопросе, несмотря на наличие в программе указаний о том, где рассматривать деформацию сдвига и закон Гука при сдвиге, так как до сих пор в ряде учебников (правда, со многими оговорками) рассматривают эти вопросы совместно с практическими ра счетами и некоторые преподаватели, к сожалению, склонны следовать указанным учебникам. [c.94]

Смотреть страницы где упоминается термин Гука закон при сдвиге : [c.84] [c.181] [c.228] [c.101] [c.104] [c.87] [c.124] Сопротивление материалов (1988) — [ c.84 ]

Сопротивление материалов Издание 3 (1969) — [ c.128 ]

Сопротивление материалов Издание 6 (1979) — [ c.74 ]

mash-xxl.info

Сдвиг. Закон Гука при чистом сдвиге. Сложное сопротивление. Косой изгиб

Страницы работы

Содержание работы

Если на гранях элемента действуют только касательные напряжение то такой вид напряженного состояния называется чистым сдвигом. Примером тела во всех точках которого имеет место чистый сдвиг является скручиваемый стержень круглого поперечного сечения. На практике деформацию чистого сдвига можно осущистьвить при кручении тонкостенной трубы.Перемещение какого либо сечения в его плоскости относительно другого параллельного ему сечения называется сдвигом. На сдвиг работают сварные и заклепочные соединения

Закон Гука при чистом сдвиге.

γ-относительная угловая деформация или угол сдвига (ввиду её малой величины tgγ=Δ/a=γ

Для многих материалов при нагружении до пределов пропорциональности пи сдвиге между напряжениями и деформациями сохраняется линейная зависимость — з. Гука при сдвиге.

γ = τ /G (G-модуль упругости 2 го рода (модуль сдвига) τ = γ* G. Он характеризует способность материалов сопротивляться деформации сдвига. По анологии з. Гука при растяжении величина линейного перемещения при сдвиге определяется по формуле.

GA-жесткость при сдвиге.

Линейная зависимость между касательными напряжениями и деформациями сохраняются до тех пор пока τ не преобретут величины предела пропорциональности. Между модулем упругости Е и модулем сдвига G и коэффициентом Пуассона μ существует зависимость

Это такой вид деформации, при котором в поперечном сечении стержня возникает не менее 2 х внутренних усилий. Исключение плоский изгиб так как в расчетах на прочность при изгибе учитываются только изгибающий момент.

Порядок расчета задач на сложное сопротивление.

В начале используя метод сечений определим внутренние усилия возникающие в поперечном сечении стержней (при сложной нагрузке рекомендуется строить эпюры внутренних усилий и определить опасные точки сечения. Затем на основании принципа суперпозиции определяем напряжения возникшие от каждого внутреннего усилия отдельно. Для этого используем ранее выведенные формулы σ=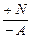; σ=M*y/I; σ_max=M_max/W) Исследуя распркделение напряжений по высоте сечения для этого строим эпюры напряжения устанавливаем опасную или предположительно опасную точкусечения для которой и составляем условие прочности. Если напряженное состояние в опасной точке является двуостным то в расчетах используем 3 и 4 теории прочности.

Косым изгибом называется такой изгиб груза когдаплоскость действия изгибающего момента в данном сечении не совпадает ни с одной из главных осей инерции. В этом случае возникающий изгибающий момент можно разложить на 2 а изгибающих момента действующих в плоскостях проходящие через главные оси инерции. То есть диф-ю косого изгиба можно првести к изибу в двух плоскостях.

На балку действует сила перпендикулярная продольной оси и составляющая сосью у некоторый угол φ.

Разложим силы на составляющие F_y=F*cos φ; F_z=F*sin φ.На расстоянии х от свободного конца балки рассмотрим сечение 1234. M_z=Fy*x; M_y=Fz*x. Используя принцип независимости действия сил определим в указанном сечении в произвольной точке А напряжение, возникшее действием силы F.

σ= σ_z+ σ_y=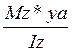 + 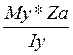=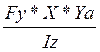+ 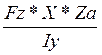(Ya и Za координаты точки А)

Используем верхние формулы. =F*X(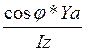+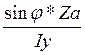). Эта формула для определения нормальных напряжений при косом изгибе в сечении где возникает изгибающий моментдля точки А.В общем виде формула имеет вид.

σ=+/-М(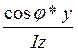+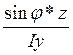) (1). Знак «-» «+» принимается исходя из физического смысла + растягивание, — сжимание.

Рассмотрим выделенное сечение 1234 и используя ф-лу 1 определим напряжение в условных точках.

Определение положение нейтральной оси при косом изгибе.

Нейтральная линия образуется пересечением нейрального слоя с плоскостью поперечного сечения σ_но=0 так как M=F*l не равно 0 то выражение в скобках (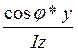+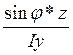)=0

Y_HO=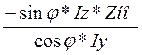 =-tgφ*Iz*Zно/Iy

tgα=-Уно/ Zно; -Zно* tgα= Уно; tgα=tgφ*Iz/Iy

В случае косого изгиба нейтральная линия не перпендикулярна линии действия силы. Положение нейтральной оси определяется углом φ и отношением Iz/Iy. Если Iz=Iy

Уно= -Zно* tgα. => в сечениях типа круг квадрат и крольцо диф-я косого изгиба не возникает.

Условие прочности при косом изгибе.

Для проверки прочности при косом изгибе необходимо установить опасное сечение, тоесть сечение где М=М_max и для точек наиболее удаленных от нейтральной оси используя формулу определения напряжения σ_max=М_max(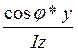+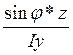)≤ [σ] (3)

В случае если материал одинаково работает на растяжение и сжатие.

Для этого составляют два уравнения прочности.Для того чтобы установить опасные точки сечения необходимо провести касательные к сечению параллельно нейтральной оси точки касания и есть опасные точки.

vunivere.ru