Закон движения и перемещения

Вернемся к определению механического движения. Определение говорит, что механическое движение есть изменение положения тел друг относительно друга с течением времени. Мы научились определять изменение положения тела как такового. Но определение механического движения требует ответа на вопросы: Когда тело будет находиться в той или иной точке траектории? Сколько времени потребуется телу, чтобы совершить то или иное перемещение? Как с течением времени меняется положение тела на траектории?

Чтобы ответить на эти вопросы, необходимо ввести в рассмотрение само время и связать его с изменениями положения тел. Для этого надо условиться о способе измерения времени и выборе начала отсчета времени. Практически это делается по-разному. Например, в спортивных соревнованиях секундомер пускают в ход в момент старта. При этом момент начала отсчета времени совпадает с моментом начала движения бегуна, и показания секундомера дают чистое время его движения.

Все виды транспорта пользуются общим отсчетом суточного астрономического времени. Чистое время движения в этом случае приходится вычислять по моментам начала и конца движения. В некоторых случаях применяется обратный отсчет времени (например, при пуске ракет, когда нуль времени совпадает с концом подготовки к пуску и с моментом старта ракеты). Эти способы задания начала отсчета времени используются и в механике.

После установления начала отсчета времени можно, наблюдая за часами, определить, в какой момент времени тело было в той или иной точке траектории, т. е. установить зависимость длины пути от времени.

Например, начало движения тела совпадало с началом отсчета длин путей (рис. 1.45). Секундомер был пущен в момент начала движения. За каждую секунду тело проходило расстояние Для этого случая зависимость длины пути от времени может быть представлена в виде таблицы:

Такая таблица позволяет ответить на все вопросы, поставленные в начале параграфа. По ней мы можем определить и положение тела для любого момента, и затраты времени, необходимые для того или иного перемещения тела. Зависимость от и получила особое название — закон движения. Итак: вид зависимости длины пути от времени называется законом движения тела по заданной траектории.

Закон движения является второй (после траектории) важнейшей общей характеристикой, дающей представление о движении в целом.

Закон движения можно задать в виде:

1) таблицы, связывающей последовательные значения длины пути с соответствующими значениями времени (именно в виде таких таблиц дают закон движения современные электронно-вычислительные цифровые машины);

2) графика зависимости длины пути от времени (иногда его называют графиком закона движения);

3) формулы, связывающей длину пути со временем

Для примера сопоставим все три формы задания закона движения.

Пусть закон некоторого движения задан таблицей, приведенной выше. Это первая форма закона движения. Данные этой таблицы позволяют построить по точкам график закона движения (рис. 1.46). Это вторая форма закона движения. Из таблицы и графика видно,

что между длиной пути и временем существует прямо пропорциональная зависимость, которая может быть передана формулой Это третья форма закона движения.

Таблица, график и формула в отдельности говорят о том, что в нашем примере: часы были пущены в момент начала движения тела; тело начало двигаться из точки начала отсчета длин путей; за равные промежутки времени тело проходило равные расстояния; двигалось в положительном направлении отсчета длин путей и фактическое время его движения совпадало с показаниями часов. Иными словами, каждая из этих форм закона дает полные ответы на все вопросы, связанные с движением тела.

Закон движения является вторым после траектории признаком (§ 10), по которому производится разделение движений на различные виды. По форме закона движения все движения разделяются на равномерные и неравнольерные.

Равномерным движением называется такое движение, в котором за любые равные промежутки времени тело проходит по траектории равные расстояния.

Рассмотренный в этом параграфе пример является одним из случаев равномерного движения.

Траектория и закон движения — независимые характеристики, и поэтому при определении любого движения необходимо указывать особенности каждой из них. Например, прямолинейное неравномерное движение, криволинейное равномерное движение, равномерное движение по окружности и т. д. Позже из неравномерных движений мы выделим особую группу равнопеременных движений.

know.sernam.ru

Способы описания движения. Система отсчета. Перемещение. — презентация

Презентация была опубликована 3 года назад пользователемМаргарита Прозорова

Похожие презентации

Презентация на тему: » Способы описания движения. Система отсчета. Перемещение.» — Транскрипт:

1 Способы описания движения. Система отсчета. Перемещение.

2 Координатный способ Если точка движется, то ее координаты изменяются с течением времени. Так как координаты точки зависят от времени, то можно сказать, что они являются функциями времени. времени -кинематические уравнения движения точки

3 Траектория движения тела Изменяя свое положение в пространстве тело движется по некоторой линии, которую называют траекторией Прямая линия ломаная кривая

4 Векторный способ. ( закон движения точки, записанный в векторной форме. векторной

5 Что необходимо для определения положения тела? 1. Тело отсчета- тело, относительно которого рассматривается движение 2. система координат, связанная с телом отсчета

6 Для определения положения движущегося объекта в любой момент времени необходимы тело отсчета, связанная с ним система координат и прибор для отсчета времени.

7 Система координат, тело отсчета, с которым она связана, прибор для измерения времени образуют систему отсчета, относительно которой рассматривается движение тела.

9 Перемещение Перемещение – это вектор, соединяющий начальное положение тела с его последующим положением. Путь – это длина участка траектории, пройденного материальной точкой за данный промежуток времени. В отличие от перемещения путь – это скалярная величина. S- перемещение, Измеряется в метрах

0, S 2X » title=»Проекция вектора перемещения на координатную ось X X0X0 X1X1 X2X2 S 1X >0, S 2X » class=»link_thumb»> 10 Проекция вектора перемещения на координатную ось X X0X0 X1X1 X2X2 S 1X >0, S 2X 0, S 2X «> 0, S 2X «> 0, S 2X » title=»Проекция вектора перемещения на координатную ось X X0X0 X1X1 X2X2 S 1X >0, S 2X «>

11 Проекция на ось считается положительной, если вектор сонаправлен с этой осью, и отрицательной, если вектор направлен противоположно оси

13 Проекция перемещения на ось ОУ

14 Модуль вектора перемещения

15 Домашнее задание П.5,6, ответить на вопросы

16 1 На рисунке показаны перемещения пяти материальных точек. Найти проекции векторов перемещения на оси координат и их модули.

17 2 Мяч упал с высоты 3 м, отскочил от пола и был пойман на высоте 1 м. Найти путь и перемещение мяча.

18 3 На рисунке показана траектория движения материальной точки из А в В. Найти координаты точки в начале и конце движения, проекции перемещения на оси координат, модуль перемещения.

19 4 Тело переместилась из точки А (2,2) в точку В ( 2,10), затем в точку С (6,10) и затем в точку Д (6,2). Найдите пройденный путь, перемещение, проекции перемещения на оси координат

20 5 Тело переместилось из точки с координатами х 1=0, y1=2 м в точку с координатами x2=4 м, y2=-1 м. Сделать чертеж, найти перемещение и его проекции на оси координат.

21 6 Катер прошел по озеру в направлении на северо-восток 2 км, а затем в северном направлении еще 1 км. Найти геометрическим построением модуль и направление перемещения звена.

22 7 Звено пионеров прошло сначала 400 м на северо-запад, затем 500 м на восток и еще 300 м на север. Найти геометрическим построением модуль и направление перемещения звена.

www.myshared.ru

Движение человека является механическим, то есть это изменение тела или его частей относительно других тел. Относительное перемещение описывает кинематика.

Кинематика – раздел механики, в котором изучается механическое движение, но не рассматриваются причины, вызывающие это движение. Описание движения как тела человека (его частей) в различных видах спорта, так и различных спортивных снарядов являются неотъемлемой частью спортивной биомеханики и в частности кинематики.

Какой бы материальный объект или явление мы не рассматривали, окажется что вне пространства и вне времени ничего не существует. Любой предмет имеет пространственные размеры и форму, находится в каком-то месте пространства по отношению к другому предмету. Любой процесс, в котором участвуют материальные объекты, имеет во времени начало и конец, сколько то длится во времени, может совершаться раньше или позже другого процесса. Именно по этому возникает необходимость измерять пространственную и временную протяжённости.

Основные единицы измерения кинематических характеристик в международной системе измерений СИ.

Пространство. Одна сорокамиллионная часть длины земного меридиана, проходящего через Париж, была названа метром. Поэтому длина измеряется в метрах (м) и кратных ему единицах измерения: километрах (км), сантиметрах (см) и т. д.

Время – одно из фундаментальных понятий. Можно сказать, что это то, что отделяет два последовательных события. Один из способов измерить время – это использовать любой регулярно повторяющийся процесс. Одна восьмидесяти шести тысячная часть земных суток была выбрана за единицу времени и была названа секундой (с) и кратных ей единицах (минутах, часах и т. д.).

В спорте используются специальные временные характеристики:

Момент времени (t) — это временная мера положения материальной точки, звеньев тела или системы тел. Моментами времени обозначают начало и окончание движения или какой либо его части или фазы.

Длительность движения (∆t) – это его временная мера, которая измеряется разностью моментов окончания и начала движения ∆t = tкон. – tнач.

Темп движения (N) – это временная мера повторности движений, повторяющихся в единицу времени. N = 1/∆t; (1/c) или (цикл/c).

Ритм движений – это временная мера соотношения частей (фаз) движений. Он определяется по соотношению длительности частей движения.

Положение тела в пространстве определяют относительно некоторой системы отсчёта, которая включает в себя тело отсчёта (то есть относительно чего рассматривается движение) и систему координат, необходимую для описания на качественном уровне положение тела в той или иной части пространства.

С телом отсчёта связывают начало и направление измерения. Например, в целом ряде соревнований началом координат можно выбрать положение старта. От него уже рассчитывают различные соревновательные дистанции во всех циклических видах спорта. Тем самым в выбранной системе координат «старт – финиш» определяют расстояние в пространстве, на которое переместится спортсмен при движении. Любое промежуточное положение тела спортсмена во время движения характеризуется текущей координатой внутри выбранного дистанционного интервала.

Для точного определения спортивного результата правилами соревнований предусматривается по какой точке (пункт отсчёта) ведётся отсчёт: по носку конька конькобежца, по выступающей точке грудной клетки бегуна-спринтера, или по заднему краю следа приземляющегося прыгуна в длину.

В некоторых случаях для точного описания движения законов биомеханики вводится понятие материальная точка.

Материальная точка – это тело, размерами и внутренней структурой которого в данных условиях можно пренебречь.

Движение тел по характеру и интенсивности могут быть различными. Чтобы охарактеризовать эти различия, в кинематике вводят ряд терминов, представленных ниже.

Траектория – линия, описываемая в пространстве движущейся точкой тела. При биомеханическом анализе движений прежде всего рассматривают траектории движений характерных точек человека. Как правило, такими точками являются суставы тела. По виду траектории движений делят на прямолинейные (прямая линия) и криволинейные (любая линия, отличная от прямой).

Перемещение – это векторная разность конечного и начального положения тела. Следовательно, перемещение характеризует окончательный результат движения.

Путь – это длина участка траектории, пройденной телом или точкой тела за выбранный промежуток времени.

Траектория движения точки и её перемещение

Для того, чтобы охарактеризовать насколько быстро изменяется в пространстве положение движущегося тела, используют специальное понятие скорость.

Скорость – это отношение пройденного пути ко времени, за который он пройден. Она показывает, как быстро изменяется положение тела в пространстве. Поскольку скорость – это вектор, то она также указывает, в каком направлении движется тело или точка тела.

Средней скоростью тела на данном участке траектории называется отношение пройденного пути ко времени движения, м/с:

Если на всех участках траектории средняя скорость одинакова, то движение называется равномерным.

Вопрос о скорости бега является важным в спортивной биомеханике. Известно, что скорость бега на определённую дистанцию зависит от величины этой дистанции. Бегун может поддерживать максимальную скорость только в течение ограниченного времени (3-4) секунды, высококвалифицированные спринтеры до 5 — 6 секунд). Средняя скорость стайеров гораздо ниже, чем спринтеров. Ниже показана зависимость средней скорости (V) от длины дистанции (S).

Зависимость средней скорости бега от длины дистанции

Мировые спортивные рекорды и показанная в них средняя скорость

Для удобства проведения вычислений среднюю скорость можно записать и через изменение координат тела. При прямолинейном движении пройденный путь равен разности координат конечной и начальной точек. Так, если в момент времени t0 тело находилось в точке с координатой Х0, а в момент времени t1 – в точке с координатой Х1, то пройденный путь ∆Х = Х1 – Х0, а время движения ∆t = t1 – t0 (символ ∆ обозначает разность однотипных величин или для обозначения очень маленьких интервалов). В этом случае:

Размерность скорости в СИ – м/с. При преодолении больших расстояний скорость определяют в км/час. При необходимости такие значения можно перевести в СИ. Например, 54 км/час = 54000 м /3600 с = 15 м/с.

Средние скорости на различных участках пути значительно отличаются даже при относительно равномерном прохождении дистанции: стартовый разгон, преодоление дистанции с внутрицикловыми колебаниями скорости (во время отталкивания скорость увеличивается, во время свободного скольжения в беге на коньках или фазы полёта в л/а беге – уменьшается), финиширование. По мере уменьшения интервала, по которому вычисляется скорость можно определить скорость в данной точке траектории, которая называется мгновенной скоростью.

Мгновенная скорость движения, или скоростью в данной точке траектории называется предел, к которому стремится перемещение тела в окрестности этой точки ко времени при неограниченном уменьшении интервала:

Мгновенная скорость – величина векторная.

Направление вектора мгновенной скорости

Если величина скорости (или модуль вектора скорости) не меняется, движение равномерное, при изменении модуля скорости – неравномерное.

Равномерным называют движение, при котором за любые равные промежутки времени тело проходит одинаковые пути. В этом случае величина скорости остаётся неизменной (по направлению скорость может изменяться, если движение криволинейное).

Прямолинейным называют движение, при котором траектория является прямой линией. В этом случае направление скорости остаётся неизменным, (величина скорости может изменяться, если движение не равномерное).

Равномерным прямолинейным называют движение, которое является и равномерным и прямолинейным. В этом случае неизменными остаются и величина и направление.

В общем случае при движении тела изменяются и величина и направление вектора скорости. Для того, чтобы охарактеризовать насколько быстро происходят эти изменения, используют специальную величину – ускорение.

Ускорение – это величина, равная отношению изменения скорости движения тела к длительности промежутка времени, за которое это изменение скорости произошло. Среднее ускорение на основе этого определения равно, м/с²:

Мгновенным ускорением называется физическая величина, равная пределу, к которому стремится среднее ускорение за промежуток ∆t → 0, м/с²:

Поскольку вдоль траектории скорость может изменяться как по величине так и по направлению, вектор ускорения имеет две составляющие.

Составляющая вектора ускорения а, направленная вдоль касательной к траектории в данной точке, называется тангенциальным ускорением, которое характеризует изменение вектора скорости по величине.

Составляющая вектора ускорения а, направленная по нормали к касательной в данной точке траектории, называется нормальным ускорением. Оно характеризует изменение вектора скорости по направлению в случае криволинейного движения. Естественно, что когда тело движется по траектории, являющейся прямой линией, нормальное ускорение равно нулю.

Прямолинейное движение называется равнопеременным, если за любые промежутки времени скорость тела изменяется на одну и ту же величину. В этом случае отношение

∆V/ ∆t одинаково для любых интервалов времени. Поэтому величина и направление ускорения остаются неизменными: а = const.

Для прямолинейного движения вектор ускорения направлен по линии движения. Если направление ускорения совпадает с направлением вектора скорости, то величина скорости будет возрастать. В этом случае движение называют равноускоренным. Если направление ускорения противоположно направлению вектора скорости, то величина скорости будет уменьшаться. В этом случае движение называют равнозамедленным. В природе существует естественное равноускоренное движение – это свободное падение.

Свободным падением – называется падение тела, если на него действует единственная сила – сила тяжести. Опыты, проведённые Галилеем, показали, что при свободном падении все тела движутся с одинаковым ускорением свободного падения и обозначаются буквой ĝ. Вблизи поверхности Земли ĝ = 9,8 м/с². Ускорение свободного падения обусловлено притяжением со стороны Земли и направлено вертикально вниз. Строго говоря, такое движение возможно лишь в вакууме. Падение в воздухе можно считать приблизительно свободным.

Траектория движения свободно падающего тела зависит от направления вектора начальной скорости. Если тело брошено вертикально вниз, то траектория – вертикальный отрезок, а движение называется равнопеременным. Если тело брошено вертикально вверх, то траектория состоит из двух вертикальных отрезков. Сначала тело поднимается, двигаясь равнозамедленно. В точке наивысшего подъёма скорость становится равной нулю, после чего тело опускается, двигаясь равноускоренно.

Если вектор начальной скорости направлен под углом к горизонту, то движение происходит по параболе. Так двигаются брошенный мяч, диск, спортсмен, прыгающий в длину, летящая пуля и др.

Движение тела, брошенного под углом к горизонту

В зависимости от формы представления кинематических параметров существуют различные виды законов движения.

Закон движения – это одна из форм определения положения тела в пространстве, которая может быть выражена:

• аналитически, то есть с помощью формул. Эта разновидность закона движения задаётся с помощью уравнений движения: x = x(t), y = y(t), z = z(t);

• графически, то есть с помощью графиков изменения координат точки в зависимости от времени;

• таблично, то есть в виде вектора данных, когда в один столбец таблицы заносят числовые отсчёты времени, а в другой в сопоставлении с первым – координаты точки или точек тела.

opace.ru

РАЗДЕЛ II. Поурочные разработки по физике к учебнику Г. Я. Мякишева, Б. Б. Буховцева, Н. Н. Сотского

ВВЕДЕНИЕ

ФИЗИКА В ПОЗНАНИИ ВЕЩЕСТВА, ПОЛЯ, ПРОСТРАНСТВА И ВРЕМЕНИ

Урок 3. Траектория. Закон движения. Перемещение. Путь

Цель урока: объяснить необходимость изучения механики; ввести понятия «траектория», «перемещения», «путь».

Давайте вспомним основные разделы физики:

Мы начнем изучение с механики, ибо относящиеся сюда явления более просты, а также потому, что знание законов механики окажет нам существенную помощь при изучении других разделов.

Механическим движением тела называется изменение с течением времени его положения по отношению к другим телам.

Приведите примеры механического движения. Например, движение людей, воды в реках и морях, движение воздуха, Земли и т. д.

— Двигайтесь ли Вы, находясь в классе? (Вы находитесь в классе в покое относительно Земли, но движетесь вместе с ним вокруг Солнца. Например, автомобиль движется относительно деревьев, зданий, но пассажиры, находящиеся в нем, находятся в покое относительно автомобиля.)

Нет абсолютно неподвижных тел. Изучая движение планет вокруг Солнца, достаточно знать движение ее центров.

Говорят, тело принимаем за материальную точку. Материальной точкой называют тело, размерами которого в рассматриваемом случае можно пренебречь.

Если траектория прямая, движение называют прямолинейным, если кривая — криволинейным.

Траектория движения указывает все положения, которые занимала точка, но, зная траекторию, ничего нельзя сказать о том, быстро или медленно проходила точка отдельные участки траектории. Чтобы получить полное описание движения, нужно знать, в какой момент точка занимала то или иное положение на траектории. Описать движение можно:

— с помощью таблиц;

Пройденное точкой расстояние, отсчитанное вдоль траектории, называется путем.

Положение материальной точки в пространстве в произвольный момент времени можно определить, если ввести систему отсчета.

Система отсчета — совокупность тела отсчета, связанной с ним системы координат и часов.

— Какие системы координат вы знаете, приведите примеры. ( Одномерные, двухмерные, трехмерные.)

Механику можно разделить на:

3. Законы сохранения.

4. Колебания и волны.

Раздел механики, в котором движения изучаются без исследования причин называют кинематикой.

Для описания движения тела нужно указать, как меняется положение точек с течением времени. При движении тела каждая его точка описывает некоторую линию — траекторию движения.

Рукопись — это траектория кончика пера. В ожидании солнечного затмения астрономы заранее вычисляют траекторию движения лунной тени по поверхности Земли.

Движение относительно траектории зависит от высоты системы отсчета. Например, в безветренную погоду струи дождя представляются вертикальными, если за ними следить из окна стоящего вагона: капли оставляют на оконных стеклах вертикальные следы, если поезд тронулся, то по отношению к идущему вагону струи дождя представляются косыми: капли будут оставлять на стеклах наклонные следы, наклон будет тем больше, чем больше скорость поезда.

Для описания движения тела нужно знать, как движутся различные точки тела. Иногда можно ограничиться описанием движения одной точки.

Системы координат: одномерные (движение автомобиля по прямой); двухмерные (шахматная фигура); трехмерные (полет мухи).

Существует материальная точка М с координатами (х, у) в момент времени t (рис. 1).

Совокупность координат х( t ) и y ( t ) в момент времени t определяет закон движения материальной точки в координатной форме, тогда положение математической точки можно задать вектором r .

Радиус-вектор — вектор, соединяющий начало отсчета с положением точки в произвольный момент времени.

Закон (или уравнение) движения в векторной форме — зависимость радиуса- вектора от времени r ( t ).

Тогда координаты связаны:

Изменение положения движущегося тела в пространстве можно характеризовать либо изменением его координат, либо изменением радиуса-вектора, так как координатные и векторные описания движения эквивалентны.

Перемещение — вектор, проведенный из начального положения материальной точки в конечное.

II. Закрепление изученного

Упражнение 1. Какую систему координат следует выбрать (одномерную, двухмерную или трехмерную) для определения положения следующих тел:

1. Трактор в поле.

4. Люстра в комнате.

6. Подводная лодка.

7. Шахматная фигура.

8. Самолет на взлетной полосе.

Задание 1. На рисунке показана дорога (повторите рисунок в тетради).

Проведите в тетради координатную ось параллельно дороге. Примите дерево за тело отсчета.

Выберите масштаб (1 деление — 100 м).

Определите координаты моста, дерева и светофора.

Определите начальные координаты пешехода, велосипедиста и автомобиля.

Покажите вектор перемещения для каждого из этих тел, его проекцию на ось Y и найдите модуль вектора перемещения, а также пройденный путь в следующих случаях:

1) автомобиль доехал до светофора;

2) пешеход дошел до дерева;

3) велосипедист доехал до светофора и вернулся к дереву.

Задание 2. Выполните те же упражнения, что и в задании 1, но за тело отсчета выберите мост.

Сравните пути и перемещения каждого из тел (полученные при выполнении заданий 1 и 2).

III . Закрепление изученного

1. В чем состоит основная задача механики?

2. Зачем введено понятие материальной точки? Когда тело можно считать материальной точкой?

3. Что такое система отсчета (СО)? Для чего вводится?

4. Какие виды систем координат (СК) вы знаете?

5. Что такое траектория?

6. В чем отличие пути от перемещения?

Кроссворд «Физические величины»

1. Наука о неживой природе. 2. Тысячная доля метра. 3. Прибор для измерения объема жидкостей. 4. Что означает греческое слово цэушы [физис], от которого произошло слово «физика»? 5. Механические, тепловые, электрические, световые явления — это явления . 6. Все, что есть во Вселенной. 7. Древнегреческий ученый. 8. «Отец» русской авиации. 9. Город, в котором в 1954 г. была построена первая в мире атомная электростанция. 10. Величина, характеризующая степень нагретости тела. 11. Русский ученый, усовершенствовавший лампы дневного света. 12. Свертывающаяся в круг металлическая или матерчатая измерительная лента с делениями. 13. Название транспортного отечественного самолета, грузоподъемностью 150 т, построенного в 1985 г. 14. Единица длины, равная 0,1 м. 15. Русский ученый и организатор, с именем которого связано развитие отечественной атомной энергетики. 16. Физическая величина, характеризующая расстояние. 17. «Он создал первый русский университет. Он, лучше сказать, сам был первым нашим университетом» (А. С. Пушкин). 18. Критерий истины.

Ответы: 1. Физика. 2. Миллиметр. 3. Мензурка. 4. Природа. 5. физические. 6. Материя. 7. Аристотель. 8. Жуковский. 9. Обнинск. 10. Температура. 11. Вавилова. 12. Рулетка. 13. Руслан. 14. Дециметр. 15. Курчатов. 16. Длина. 17. Ломоносов. 18. Опыт.

www.compendium.su

Закон движения и перемещения

Любое физическое явление или процесс в окружающем нас материальном мире представляет собой закономерный ряд изменений, происходящих во времени и пространстве. Механическое движение, то есть изменение положения данного тела (или его частей) относительно других тел, – это простейший вид физического процесса. Механическое движение тел изучается в разделе физики, который называется механикой . Основная задача механики – определить положение тела в любой момент времени .

Одна из основных частей механики, которая называется кинематикой , рассматривает движение тел без выяснения причин этого движения. Кинематика отвечает на вопрос: как движется тело? Другой важной частью механики является динамика , которая рассматривает действе одних тел на другие как причину движения. Динамика отвечает на вопрос: почему тело движется именно так, а не иначе?

Механика – одна из самых древних наук. Определенные познания в этой области были известны задолго до новой эры (Аристотель (IV век до н. э.), Архимед (III в. до н.э.)). Однако, качественная формулировка законов механики началась только в XVII веке н. э., когда Г. Галилей открыл кинематический закон сложения скоростей и установил законы свободного падения тел. Через несколько десятилетий после Галилея великий И. Ньютон (1643–1727) сформулировал основные законы динамики.

В механике Ньютона движение тел рассматривается при скоростях, много меньше скорости света в пустоте. Ее называют классической или ньютоновской механикой в отличие от релятивистской механики, созданной в начале XX века главным образом благодаря работам А. Эйнштейна (1879–1956).

В релятивистской механике движение тел рассматривается при скоростях, близких к скорости света. Классическая механика Ньютона является предельным случаем релятивистской при υ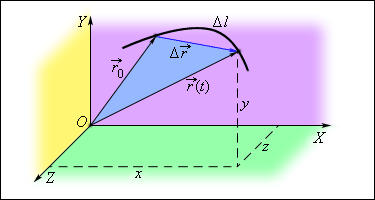

Перемещением тела 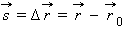называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. Перемещение есть векторная величина.

Пройденный путь l равен длине дуги траектории, пройденной телом за некоторое время t . Путь – скалярная величина.

Если движение тела рассматривать в течение достаточно короткого промежутка времени, то вектор перемещения окажется направленным по касательной к траектории в данной точке, а его длина будет равна пройденному пути.

В случае достаточно малого промежутка времени Δ t пройденный телом путь Δ l почти совпадает с модулем вектора перемещения 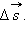При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути (рис. 1.1.2).

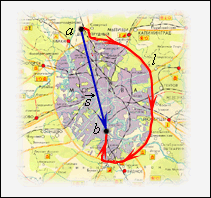
Для характеристики движения вводится понятие средней скорости :

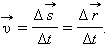
В физике наибольший интерес представляет не средняя, а мгновенная скорость , которая определяется как предел, к которому стремится средняя скорость на бесконечно малом промежутке времени Δ t :

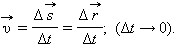
В математике такой предел называют производной и обозначают 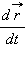или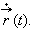

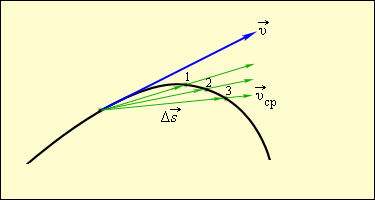
Мгновенная скорость 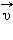тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке. Различие между средней и мгновенной скоростями показано на рис. 1.1.3.

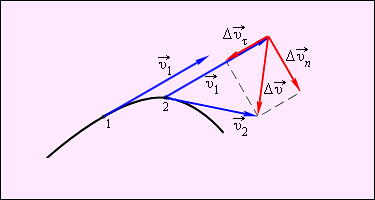
При движении тела по криволинейной траектории его скорость 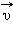изменяется по модулю и направлению. Изменение вектора скорости 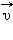за некоторый малый промежуток времени Δ t можно задать с помощью вектора 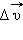(рис. 1.1.4).

Вектор изменения скорости 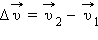за малое время Δ t можно разложить на две составляющие: 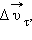направленную вдоль вектора 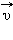(касательная составляющая), и 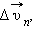направленную перпендикулярно вектору 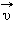(нормальная составляющая).

Мгновенным ускорением (или просто ускорением ) 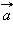тела называют предел отношения малого изменения скорости 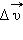к малому промежутку времени Δ t , в течение которого происходило изменение скорости:

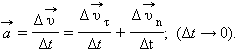
Направление вектора ускорения 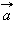в случае криволинейного движения не совпадает с направлением вектора скорости 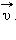Составляющие вектора ускорения 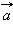называют касательным ( тангенциальным ) 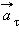и нормальным 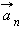ускорениями (рис. 1.1.5).

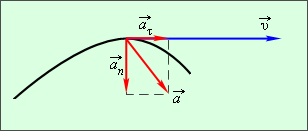
Касательное ускорение указывает, насколько быстро изменяется скорость тела по модулю:

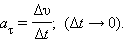
Вектор 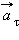направлен по касательной к траектории.

Нормальное ускорение указывает, насколько быстро скорость тела изменяется по направлению.

Криволинейное движение можно представить как движение по дугам окружностей (рис. 1.1.6).

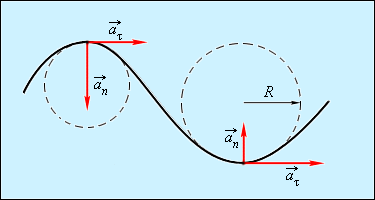
Нормальное ускорение зависит от модуля скорости υ и от радиуса R окружности, по дуге которой тело движется в данный момент:

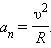
Вектор 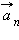всегда направлен к центру окружности (см. §1.6).

Из рис. 1.1.5 видно, что модуль полного ускорения равен

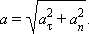
Таким образом, основными физическими величинами в кинематике материальной точки являются пройденный путь l , перемещение 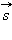, скорость 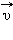и ускорение 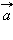. Путь l является скалярной величиной. Перемещение 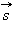, скорость 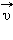и ускорение 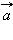– величины векторные. Чтобы задать векторную величину, нужно задать ее модуль и указать направление. Векторные величины подчиняются определенным математическим правилам. Вектора можно проектировать на координатные оси, их можно складывать, вычитать и т. д.

physics.ru