Закон колебания тока

Тема 10. «Электромагнитные колебания и волны».

ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ.
СВОБОДНЫЕ И ВЫНУЖДЕННЫЕ ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ.

Электромагнитные колебания — взаимосвязанные колебания электрического и магнитного полей.

Электромагнитные колебания появляются в различных электрических цепях. При этом колеблются величина заряда, напряжение, сила тока, напряженность электрического поля, индукция магнитного поля и другие электродинамические величины.

Свободные электромагнитные колебания возникают в электромагнитной системе после выведения ее из состояния равновесия, например, сообщением конденсатору заряда или изменением тока в участке цепи.

Это затухающие колебания, так как сообщенная системе энергия расходуется на нагревание и другие процессы.

Вынужденные электромагнитные колебания — незатухающие колебания в цепи, вызванные внешней периодически изменяющейся синусоидальной ЭДС.

Электромагнитные колебания описываются теми же законами, что и механические, хотя физическая природа этих колебаний совершенно различна.

Электрические колебания — частный случай электромагнитных, когда рассматривают колебания только электрических величин. В этом случае говорят о переменных токе, напряжении, мощности и т.д.

Колебательный контур — электрическая цепь, состоящая из последовательно соединенных конденсатора емкостью C, катушки индуктивностью L и резистора сопротивлением R.

Состояние устойчивого равновесия колебательного контура характеризуется минимальной энергией электрического поля (конденсатор не заряжен) и магнитного поля (ток через катушку отсутствует).

Величины, выражающие свойства самой системы (параметры системы): L и m, 1/C и k

величины, характеризующие состояние системы:

величины, выражающие скорость изменения состояния системы: u = x'(t) и i = q'(t) .

ХАРАКТЕРИСТИКИ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ

Можно показать, что уравнение свободных колебаний для зарядаq = q(t) конденсатора в контуре имеет вид

где q» — вторая производная заряда по времени. Величина

является циклической частотой. Такими же уравнениями описываются колебания тока, напряжения и других электрических и магнитных величин.

Одним из решений уравнения (1) является гармоническая функция

Период колебаний в контуре дается формулой (Томсона):

Величина φ = ώt + φ₀, стоящая под знаком синуса или косинуса, является фазой колебания.

Фаза определяет состояние колеблющейся системы в любой момент времени t.

Ток в цепи равен производной заряда по времени, его можно выразить

Чтобы нагляднее выразить сдвиг фаз, перейдем от косинуса к синусу

ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК

1. Гармоническая ЭДС возникает, например, в рамке, которая вращается с постоянной угловой скоростью в однородном магнитном поле с индукцией В. Магнитный поток Ф , пронизывающий рамку с площадью S ,

где- угол между нормалью к рамке и вектором магнитной индукции .

По закону электромагнитной индукции Фарадея ЭДС индукции равна

где — скорость изменения потока магнитной индукции.

Гармонически изменяющийся магнитный поток вызывает синусоидальную ЭДС индукции

где — амплитудное значение ЭДС индукции.

2. Если к контуру подключить источник внешней гармонической ЭДС

то в нем возникнут вынужденные колебания, происходящие с циклической частотой ώ, совпадающей с частотой источника.

При этом вынужденные колебания совершают заряд q, разность потенциалов u , сила тока i и другие физические величины. Это незатухающие колебания, так как к контуру подводится энергия от источника, которая компенсирует потери. Гармонически изменяющиеся в цепи ток, напряжение и другие величины называют переменными. Они, очевидно, изменяются по величине и направлению. Токи и напряжения, изменяющиеся только по величине, называют пульсирующими.

В промышленных цепях переменного тока России принята частота 50 Гц.

Для подсчета количества теплоты Q, выделяющейся при прохождении переменного тока по проводнику с активным сопротивлением R, нельзя использовать максимальное значение мощности, так как оно достигается только в отдельные моменты времени. Необходимо использовать среднюю за период мощность — отношение суммарной энергии W, поступающей в цепь за период, к величине периода:

Поэтому количество теплоты, выделится за время Т:

Действующее значение I силы переменного тока равно силе такого постоянного тока, который за время, равное периоду T, выделяет такое же количество теплоты, что и переменный ток:

Отсюда действующее значение тока

Аналогично действующее значение напряжения

Трансформатор — устройство, увеличивающее или уменьшающее напряжение в несколько раз практически без потерь энергии.

Трансформатор состоит из стального сердечника, собранного из отдельных пластин, на котором крепятся две катушки с проволочными обмотками. Первичная обмотка подключается к источнику переменного напряжения, а к вторичной присоединяют устройства, потребляющие электроэнергию.

называют коэффициентом трансформации. Для понижающего трансформатора К > 1, для повышающего К 3 А, ток изменяется по закону:

i=-5000 sin100t

www.yaklass.ru

Гармонические колебания в электрическом контуре

Рассмотрим замкнутую электрическую цепь, состоящую из конденсатора емкостью С и катушки индуктивностью L, без активного сопротивления. Такая цепь называется идеальным колебательным контуром.

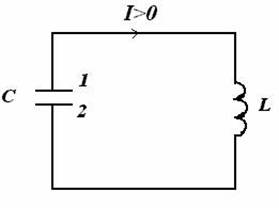
Если конденсатор был предварительно заряжен, то после замыкания цепи в ней пойдет ток. Закон Ома для участка цепи 1 — L — 2 запишется следующим образом:

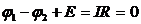
где Е — э.д.с. самоиндукции.

Если в этом уравнении сделать подстановки:

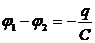
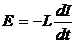
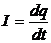
то придем к следующему уравнению относительно заряда q:

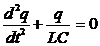
Сравнивая его с уравнением свободных гармонических колебаний, видим, что полученное уравнение также является уравнением свободных гармонических колебаний заряда на обкладках конденсатора с циклической частотой:

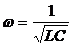
Колебания заряда в контуре происходят по закону:

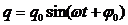
а колебания тока —

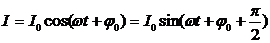
В этих формулах: q₀ — амплитуда заряда, I₀ — амплитуда тока,

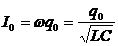
Ток в контуре опережает заряд конденсатора по фазе на p /2.

Разность потенциалов на обкладках конденсатора также меняется по синусоидальному закону (синхронно с колебаниями заряда):

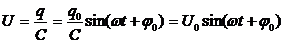
Амплитуду тока можно выразить через амплитуду напряжения:

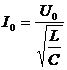
В таком виде формула напоминает закон Ома, а размерность знаменателя соответствует размерности сопротивления. Поэтому величину, стоящую в знаменателе называют волновым сопротивлением контура. Это сопротивление не следует путать с активным сопротивлением R (которого в нашем идеализированном контуре нет). Сопротивление изменяющемуся току оказывают не столкновения носителей заряда (электронов) в проводнике с ионами кристаллической решетки с безвозвратной потерей электромагнитной энергии, а э.д.с. самоиндукции в катушке в соответствии с законом

1791 — 1867

koi.tspu.ru

Закон колебания тока

В технике и в окружающем нас мире часто приходится сталкиваться с периодическими (или почти периодическими ) процессами, которые повторяются через одинаковые промежутки времени. Такие процессы называют колебательными . Колебательные явления различной физической природы подчиняются общим закономерностям. Например, колебания тока в электрической цепи и колебания математического маятника могут описываться одинаковыми уравнениями. Общность колебательных закономерностей позволяет рассматривать колебательные процессы различной природы с единой точки зрения.

Механическими колебаниями называются периодические (или почти периодические) изменения физической величины, описывающей механическое движение (скорость, перемещение, кинетическая и потенциальныая энергия и т. п.).

Если в какой-либо точке среды, в которой близко расположенные атомы или молекулы испытывают силовое воздействие, возбужден процесс механических колебаний, то этот процесс будет с конечной скоростью, зависящей от свойств среды, распространяться от точки к точке. Так возникают механические волны . Примерами такого процесса являются звуковые волны в воздухе.

Как и колебания, волновые процессы различной физической природы (звук, электромагнитные волны, волны на поверхности жидкости и т. д.) имеют много общего. Распространение волн различной физической природы можно описывать с помощью одинаковых математических уравнений. В этом проявляется единство материального мира.

Механические колебания

2.1. Гармонические колебания

Наряду с поступательными и вращательными движениями тел в механике значительный интерес представляют и колебательные движения. Механическими колебаниями называют движения тел, повторяющиеся точно (или приблизительно) через одинаковые промежутки времени. Закон движения тела, совершающего колебания, задается с помощью некоторой периодической функции времени x = f ( t ) . Графическое изображение этой функции дает наглядное представление о протекании колебательного процесса во времени.

Примерами простых колебательных систем могут служить груз на пружине или математический маятник (рис. 2.1.1).

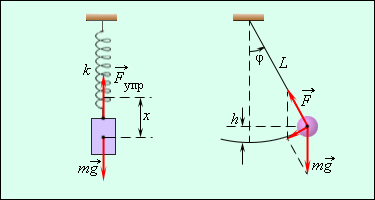
Механические колебания, как и колебательные процессы любой другой физической природы, могут быть свободными и вынужденными . Свободные колебания совершаются под действием внутренних сил системы, после того, как система была выведена из состояния равновесия. Колебания груза на пружине или колебания маятника являются свободными колебаниями. Колебания, происходящие под действием внешних периодически изменяющихся сил, называются вынужденными (см. §2.5).

Простейшим видом колебательного процесса являются простые гармонические колебания , которые описываются уравнением

Здесь x – смещение тела от положения равновесия, x _m – амплитуда колебаний, т. е. максимальное смещение от положения равновесия, ω – циклическая или круговая частота колебаний, t – время. Величина, стоящая под знаком косинуса φ = ω t + φ₀ называется фазой гармонического процесса. При t = 0 φ = φ₀ , поэтому φ₀ называют начальной фазой . Минимальный интервал времени, через который происходит повторение движения тела, называется периодом колебаний T . Физическая величина, обратная периоду колебаний, называется частотой колебаний :

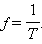
Частота колебаний f показывает, сколько колебаний совершается за 1 с . Единица частоты – герц ( Гц ). Частота колебаний f связана с циклической частотой ω и периодом колебаний T соотношениями:

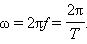
На рис. 2.1.2 изображены положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить экспериментально при освещении колеблющегося тела короткими периодическими вспышками света ( стробоскопическое освещение ). Стрелки изображают векторы скорости тела в различные моменты времени.

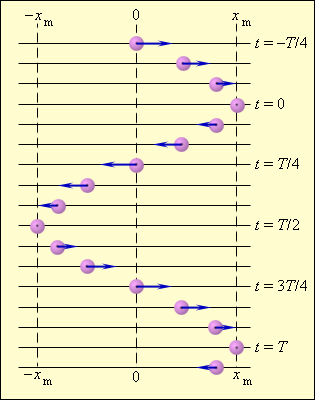
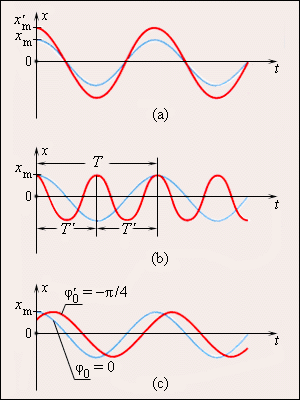
Рис. 2.1.3 иллюстрирует изменения, которые происходят на графике гармонического процесса, если изменяются либо амплитуда колебаний x _m, либо период T (или частота f ), либо начальная фаза φ₀ .

При колебательном движении тела вдоль прямой линии (ось OX ) вектор скорости направлен всегда вдоль этой прямой. Скорость υ = υ _x движения тела определяется выражением

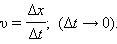
В математике процедура нахождения предела отношения 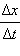при Δ t → 0 называется вычислением производной функции x ( t ) по времени t и обозначается как 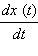или как x’ ( t ) или, наконец, как 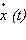. Для гармонического закона движения 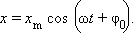Вычисление производной приводит к следующему результату:

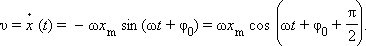
Появление слагаемого + π / 2 в аргументе косинуса означает изменение начальной фазы. Максимальные по модулю значения скорости υ = ω x _m достигаются в те моменты времени, когда тело проходит через положения равновесия ( x = 0 ). Аналогичным образом определяется ускорение a = a _x тела при гармонических колебаниях:

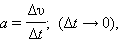
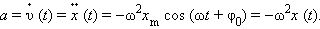
Знак минус в этом выражении означает, что ускорение a ( t ) всегда имеет знак, противоположный знаку смещения x ( t ) , и, следовательно, по второму закону Ньютона сила, заставляющая тело совершать гармонические колебания, направлена всегда в сторону положения равновесия ( x = 0 ).

На рис. 2.1.4 приведены графики координаты, скорости и ускорения тела, совершающего гармонические колебания.

physics.ru

I. Механика

Тестирование онлайн

Гармоническое колебание

Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.

График гармонического колебания

График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.

Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.

Уравнение гармонического колебания

Уравнение гармонического колебания устанавливает зависимость координаты тела от времени

График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой .

Изменение скорости и ускорения при гармоническом колебании

Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия — достигает максимального значения.

Если колебание описывать по закону косинуса

Если колебание описывать по закону синуса

Максимальные значения скорости и ускорения

Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле

Как получить зависимости v(t) и a(t)

Формулы зависимостей скорости от времени и ускорения от времени можно получить математически, зная зависимость координаты от времени. Аналогично равноускоренному движению, зависимость v(t) — это первая производная x(t). А зависимость a(t) — это вторая производная x(t).

При нахождении производной предполагаем, что переменной (то есть x в математике) является t, остальные физические величины воспринимаем как постоянные.

fizmat.by

Электромагнитные колебания

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: свободные электромагнитные колебания, колебательный контур, вынужденные электромагнитные колебания, резонанс, гармонические электромагнитные колебания.

Электромагнитные колебания — это периодические изменения заряда, силы тока и напряжения, происходящие в электрической цепи. Простейшей системой для наблюдения электромагнитных колебаний служит колебательный контур.

Колебательный контур

Колебательный контур — это замкнутый контур, образованный последовательно соединёнными конденсатором и катушкой.

Зарядим конденсатор, подключим к нему катушку и замкнём цепь. Начнут происходить свободные электромагнитные колебания — периодические изменения заряда на конденсаторе и тока в катушке. Свободными, напомним, эти колебания называются потому, что они совершаются без какого-либо внешнего воздействия — только за счёт энергии, запасённой в контуре.

Период колебаний в контуре обозначим, как всегда, через . Сопротивление катушки будем считать равным нулю.

Рассмотрим подробно все важные стадии процесса колебаний. Для большей наглядности будем проводить аналогию с колебаниями горизонтального пружинного маятника.

Начальный момент: . Заряд конденсатора равен , ток через катушку отсутствует (рис. 1 ). Конденсатор сейчас начнёт разряжаться.

Несмотря на то, что сопротивление катушки равно нулю, ток не возрастёт мгновенно. Как только ток начнёт увеличиваться, в катушке возникнет ЭДС самоиндукции, препятствующая возрастанию тока.

Аналогия. Маятник оттянут вправо на величину и в начальный момент отпущен. Начальная скорость маятника равна нулю.

Первая четверть периода : . Конденсатор разряжается, его заряд в данный момент равен . Ток через катушку нарастает (рис. 2 ).

Увеличение тока происходит постепенно: вихревое электрическое поле катушки препятствует нарастанию тока и направлено против тока.

Аналогия . Маятник движется влево к положению равновесия; скорость маятника постепенно увеличивается. Деформация пружины (она же — координата маятника) уменьшается.

Конец первой четверти : . Конденсатор полностью разрядился. Сила тока достигла максимального значения (рис. 3 ). Сейчас начнётся перезарядка конденсатора.

Напряжение на катушке равно нулю, но ток не исчезнет мгновенно. Как только ток начнёт уменьшаться, в катушке возникнет ЭДС самоиндукции, препятствующая убыванию тока.

Аналогия. Маятник проходит положение равновесия. Его скорость достигает максимального значения . Деформация пружины равна нулю.

Вторая четверть: . Конденсатор перезаряжается — на его обкладках появляется заряд противоположного знака по сравнению с тем, что был вначале (рис. 4 ).

Сила тока убывает постепенно: вихревое электрическое поле катушки, поддерживая убывающий ток, сонаправлено с током.

Аналогия. Маятник продолжает двигаться влево — от положения равновесия к правой крайней точке. Скорость его постепенно убывает, деформация пружины увеличивается.

Конец второй четверти . Конденсатор полностью перезарядился, его заряд опять равен (но полярность другая). Сила тока равна нулю (рис. 5 ). Сейчас начнётся обратная перезарядка конденсатора.

Аналогия. Маятник достиг крайней правой точки. Скорость маятника равна нулю. Деформация пружины максимальна и равна .

Третья четверть: . Началась вторая половина периода колебаний; процессы пошли в обратном направлении. Конденсатор разряжается (рис. 6 ).

Аналогия. Маятник двигается обратно: от правой крайней точки к положению равновесия.

Конец третьей четверти: . Конденсатор полностью разрядился. Ток максимален и снова равен , но на сей раз имеет другое направление (рис. 7 ).

Аналогия. Маятник снова проходит положение равновесия с максимальной скоростью , но на сей раз в обратном направлении.

Четвёртая четверть: . Ток убывает, конденсатор заряжается (рис. 8 ).

Аналогия. Маятник продолжает двигаться вправо — от положения равновесия к крайней левой точке.

Конец четвёртой четверти и всего периода: . Обратная перезарядка конденсатора завершена, ток равен нулю (рис. 9 ).

Данный момент идентичен моменту , а данный рисунок — рисунку 1 . Совершилось одно полное колебание. Сейчас начнётся следующее колебание, в течение которого процессы будут происходить точно так же, как описано выше.

Аналогия. Маятник вернулся в исходное положение.

Рассмотренные электромагнитные колебания являются незатухающими — они будут продолжаться бесконечно долго. Ведь мы предположили, что сопротивление катушки равно нулю!

Точно так же будут незатухающими колебания пружинного маятника при отсутствии трения.

В реальности катушка обладает некоторым сопротивлением. Поэтому колебания в реальном колебательном контуре будут затухающими. Так, спустя одно полное колебание заряд на конденсаторе окажется меньше исходного значения. Со временем колебания и вовсе исчезнут: вся энергия, запасённая изначально в контуре, выделится в виде тепла на сопротивлении катушки и соединительных проводов.

Точно так же будут затухающими колебания реального пружинного маятника: вся энергия маятника постепенно превратится в тепло из-за неизбежного наличия трения.

Энергетические превращения в колебательном контуре

Продолжаем рассматривать незатухающие колебания в контуре, считая сопротивление катушки нулевым. Конденсатор имеет ёмкость , индуктивность катушки равна .

Поскольку тепловых потерь нет, энергия из контура не уходит: она постоянно перераспределяется между конденсатором и катушкой.

Возьмём момент времени, когда заряд конденсатора максимален и равен , а ток отсутствует. Энергия магнитного поля катушки в этот момент равна нулю. Вся энергия контура сосредоточена в конденсаторе:

Теперь, наоборот, рассмотрим момент, когда ток максимален и равен , а конденсатор разряжен. Энергия конденсатора равна нулю. Вся энергия контура запасена в катушке:

В произвольный момент времени, когда заряд конденсатора равен и через катушку течёт ток , энергия контура равна:

Соотношение (1) применяется при решении многих задач.

Электромеханические аналогии

В предыдущем листке про самоиндукцию мы отметили аналогию между индуктивностью и массой. Теперь мы можем установить ещё несколько соответствий между электродинамическими и механическими величинами.

Для пружинного маятника мы имеем соотношение, аналогичное (1) :

Здесь, как вы уже поняли, — жёсткость пружины, — масса маятника, и — текущие значения координаты и скорости маятника, и — их наибольшие значения.

Сопоставляя друг с другом равенства (1) и (2) , мы видим следующие соответствия:

Опираясь на эти электромеханические аналогии, мы можем предвидеть формулу для периода электромагнитных колебаний в колебательном контуре.

В самом деле, период колебаний пружинного маятника, как мы знаем, равен:

B соответствии с аналогиями (5) и (6) заменяем здесь массу на индуктивность , а жёсткость на обратную ёмкость . Получим:

Электромеханические аналогии не подводят: формула (7) даёт верное выражение для периода колебаний в колебательном контуре. Она называется формулой Томсона. Мы вскоре приведём её более строгий вывод.

Гармонический закон колебаний в контуре

Напомним, что колебания называются гармоническими, если колеблющаяся величина меняется со временем по закону синуса или косинуса. Если вы успели забыть эти вещи, обязательно повторите листок «Механические колебания».

Колебания заряда на конденсаторе и силы тока в контуре оказываются гармоническими. Мы сейчас это докажем. Но прежде нам надо установить правила выбора знака для заряда конденсатора и для силы тока — ведь при колебаниях эти величины будут принимать как положительные, так и отрицательные значения.

Сначала мы выбираем положительное направление обхода контура. Выбор роли не играет; пусть это будет направление против часовой стрелки (рис. 10 ).

Рис. 10. Положительное направление обхода

Сила тока считается положительной 0)’ class=’tex’ alt='(I > 0)’ /> , если ток течёт в положительном направлении. В противном случае сила тока будет отрицательной .

Заряд конденсатора — это заряд той его пластины, на которую течёт положительный ток (т. е. той пластины, на которую указывает стрелка направления обхода). В данном случае — заряд левой пластины конденсатора.

При таком выборе знаков тока и заряда справедливо соотношение: (при ином выборе знаков могло случиться ). Действительно, знаки обеих частей совпадают: если 0′ class=’tex’ alt=’I > 0′ /> , то заряд левой пластины возрастает, и потому 0′ class=’tex’ alt=’\dot > 0′ /> .

Величины и меняются со временем, но энергия контура остаётся неизменной:

Стало быть, производная энергии по времени обращается в нуль: . Берём производную по времени от обеих частей соотношения (8) ; не забываем, что слева дифференцируются сложные функции (Если — функция от , то по правилу дифференцирования сложной функции производная от квадрата нашей функции будет равна: ):

Подставляя сюда и , получим:

Но сила тока не является функцией, тождественно равной нулю; поэтому

Перепишем это в виде:

Мы получили дифференциальное уравнение гармонических колебаний вида , где . Это доказывает, что заряд конденсатора колеблется по гармоническому закону (т.е. по закону синуса или косинуса). Циклическая частота этих колебаний равна:

Эта величина называется ещё собственной частотой контура; именно с этой частотой в контуре совершаются свободные (или, как ещё говорят, собственные колебания). Период колебаний равен:

Мы снова пришли к формуле Томсона.

Гармоническая зависимость заряда от времени в общем случае имеет вид:

Циклическая частота находится по формуле (10) ; амплитуда и начальная фаза определяются из начальных условий.

Мы рассмотрим ситуацию, подробно изученную в начале этого листка. Пусть при заряд конденсатора максимален и равен (как на рис. 1 ); ток в контуре отсутствует. Тогда начальная фаза , так что заряд меняется по закону косинуса с амплитудой :

Найдём закон изменения силы тока. Для этого дифференцируем по времени соотношение (12) , опять-таки не забывая о правиле нахождения производной сложной функции:

Мы видим, что и сила тока меняется по гармоническому закону, на сей раз — по закону синуса:

Амплитуда силы тока равна:

Наличие «минуса» в законе изменения тока (13) понять не сложно. Возьмём, к примеру, интервал времени (рис. 2 ).

Ток течёт в отрицательном направлении: . Поскольку , фаза колебаний находится в первой четверти: . Синус в первой четверти положителен; стало быть, синус в (13) будет положительным на рассматриваемом интервале времени. Поэтому для обеспечения отрицательности тока действительно необходим знак «минус» в формуле (13) .

А теперь посмотрите на рис. 8 . Ток течёт в положительном направлении. Как же работает наш «минус» в этом случае? Разберитесь-ка, в чём тут дело!

Изобразим графики колебаний заряда и тока, т.е. графики функций (12) и (13) . Для наглядности представим эти графики в одних координатных осях (рис. 11 ).

Рис. 11. Графики колебаний заряда и тока

Обратите внимание: нули заряда приходятся на максимумы или минимумы тока; и наоборот, нули тока соответствуют максимумам или минимумам заряда.

Используя формулу приведения

запишем закон изменения тока (13) в виде:

Сопоставляя это выражение с законом изменения заряда , мы видим, что фаза тока, равная , больше фазы заряда на величину . В таком случае говорят, что ток опережает по фазе заряд на ; или сдвиг фаз между током и зарядом равен ; или разность фаз между током и зарядом равна .

Опережение током заряда по фазе на графически проявляется в том, что график тока сдвинут влево на относительно графика заряда. Сила тока достигает, например, своего максимума на четверть периода раньше, чем достигает максимума заряд (а четверть периода как раз и соответствует разности фаз ).

Вынужденные электромагнитные колебания

Как вы помните, вынужденные колебания возникают в системе под действием периодической вынуждающей силы. Частота вынужденных колебаний совпадает с частотой вынуждающей силы.

Вынужденные электромагнитные колебания будут совершаться в контуре, поключённом к источнику синусоидального напряжения (рис. 12 ).

Рис. 12. Вынужденные колебания

Если напряжение источника меняется по закону:

то в контуре происходят колебания заряда и тока с циклической частотой (и с периодом, соответственно, ). Источник переменного напряжения как бы «навязывает» контуру свою частоту колебаний, заставляя забыть о собственной частоте .

Амплитуда вынужденных колебаний заряда и тока зависит от частоты : амплитуда тем больше,чем ближе к собственной частоте контура .При наступает резонанс — резкое возрастание амплитуды колебаний. Мы поговорим о резонансе более подробно в следующем листке, посвящённом переменному току.

ege-study.ru